Welcome to FengHZ's Blog!
-
Git 学习笔记
Git学习内容:多分支与回退版本
学习目的
1.弄清楚如何创建分支,合并分支,以及分支开发到一半回退回主枝
2.弄清楚如何把文件回退到指定的版本
本学习所有内容都来自于网站Git Book 中文版中chap 2-3 ,7的内容
-
Speed/accuracy trade-offs for modern convolutional object detectors 阅读笔记
论文题目:Speed/accuracy trade-offs for modern convolutional object detectors
提纲
论文立足于一个基本问题,即我们如何衡量object detector的性价比。先前的论文以及它们所提出的新结构都是基于如何提高准确率的问题,而唯一涉及到efficiency的话题就是one stage or two stage detectors.从一般经验上来说,one stage detector肯定比two stage detector要快,但是精度比后者高。但是这是一个定性的结论,在应用到具体问题的时候,往往不能提供具体的定量帮助。

-
R-FCN:Object Detection via Region-based Fully Convolutional Networks阅读笔记
论文题目:R-FCN:Object Detection via Region-based Fully Convolutional Networks
论文概要
论文主要是对Faster R-CNN的一个修改,即使用全部都是卷积,没有全连接的网络来进行Object Detection任务,而它针对的问题就是Faster R-CNN进行Feature projection与ROI Pooling后需要对很多Pooling后的重复特征进行全连接的问题,这里的计算量很大,而该文章就是要解决这个问题。
-
Mask R-CNN 阅读笔记
论文题目: Mask R-CNN
论文概要
论文立足于Instance Segmentation问题,提出了Mask R-CNN架构以解决该问题。传统的做法一般是将区域找出来了然后再分类,但是Mask R-CNN提出的思想是将BBox Regression,Classification and Segmentation并行发展,也就是说最后我们会同时获得BBox调整的参数,当前BBox的分类以及当前BBox的二值分割。整个文章可以着眼于以下3个问题上:
- Mask R-CNN的框架是什么样的
- 什么是ROI Align,它应该如何具体计算
- 如何将分割与ground truth相对应
-
DBSCAN 学习笔记
报告题目:Learn DBSCAN
算法
整个算法的目标就是去识别稠密区域。如何定义稠密呢?可以认为是对一个给定点周围的object的数目。这就导致了对于DBSCAN有2个重要参数,一个是epsilon,另外一个是minimum points 。
-
Focal Loss阅读笔记
论文题目:Focal Loss
论文概要
论文面向one stage的网络,提出了focal loss以解决one stage网络比不上two stage的表现的问题。整个文章可以着眼于以下两个问题上:
- 什么是Focal Loss,它是怎么起作用的
- 作者用了什么样的结构,并在这个结构中使用了Focal Loss达到了state of art的成果
-
Deep Adversarial Network 相关笔记
报告题目: Deep Adversarial Network Reading Recordings
序言与笔记大纲
为了做关于Deep Adversarial Network的相关研究,我认真阅读了文献[1],[2],并顺带阅读了文献[3]以及文献[4]写作了这篇报告。
我的报告主要想要结合以下几个问题展开:
- 文献[1]想要解决什么样的问题
- 文献[2]在文献[1]的基础上进行了什么样的改动,并完成了什么样的问题
- 文献[1],文献[2]在解决问题的过程中遇到了什么样的困难,它们是如何解决这些困难的
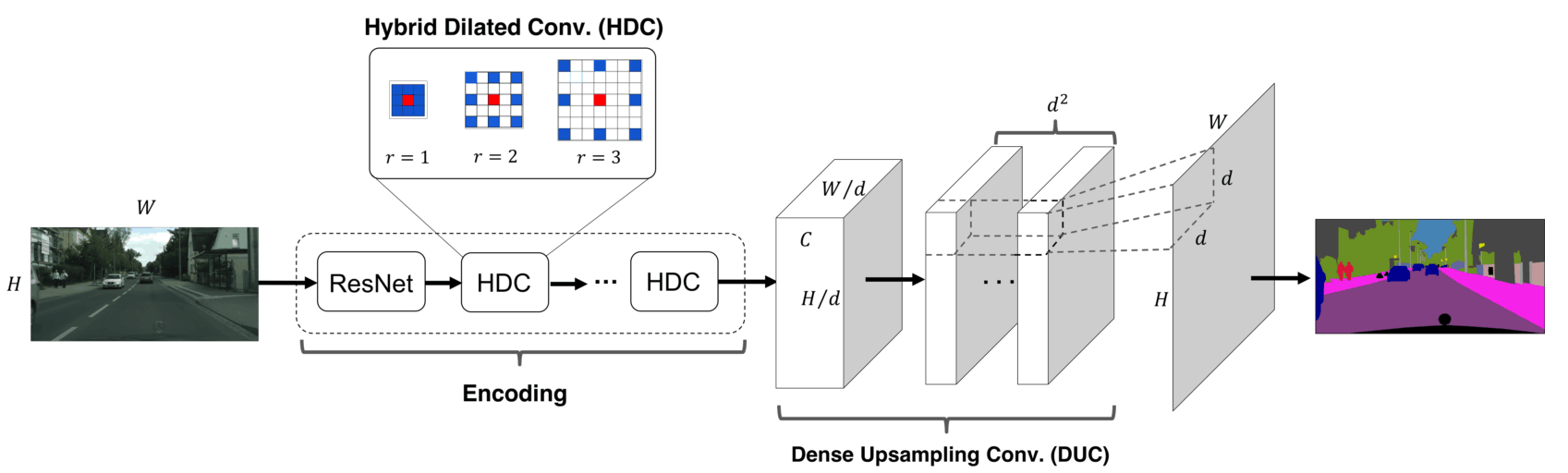
- 文献[3]与文献[4]所提到的关于语义分割的主流是什么,这些部分对我的工作是否有用。
- 我的下一步工作重心与工作目的是什么
读完报告的目的应该是我从头到尾就可以把整个网络给复现出来,里面的参数设置与细节也一清二楚。
-
PEP8 命名风格学习
-
Calculus Chap.3
自我介绍
什么是微积分
函数是人类第一次对自然规律的抽象体现,而微积分是一门研究连续变化的函数的学科。
为了判断函数是不是连续的,微积分引入了极限的概念,并指出函数是连续的当且仅当$\forall x,lim_{x’\rightarrow x}f(x’)=f(x)$。
因为函数是连续变化的,因此我们可以研究函数在某一点的变化趋势,这个变化趋势包括变化的方向,变化的快慢,变化的转折(函数极值)。因此我们引入了微分。微分给出了我们对于复杂函数的局部用简单的线性函数与多项式函数进行逼近的可能性,法则与误差分析,这是它的工程意义。
同时在研究微分的时候,我们需要考虑它的逆运算,即给定一个连续函数$f$,它可以成为什么样的函数的导数呢?($F’(x)=f(x)$)
在定义了微分与积分的运算后,我们对它们分配了不同的记号$d,\int$,这些记号可以作用在函数上$\frac{df}{dx},\int f dx$。
一个很自然的问题是,这些运算与我们常用的四则运算有什么样的不同之处?这些运算满足交换律,结合律,分配律吗?这些运算在什么情况下能用,什么情况下不能用?针对这些情况我们进行了讨论,并给出了微积分运算的一些规律。
以上组成了整个微积分的体系。
为什么要学好微积分
金融,经济,管理
AI,CS
Data Science
还有概率论与数理统计等后续课程
还有计量经济学,中微高微中宏高宏等课程
微积分都是基石
如何学好微积分
首先,无论如何都要形成对某种定理的数学直观。
其次,多做题。一道定理十道题。
如何及格
- 老师划过的课后习题刷一遍
- 历年试卷刷一遍
- 按时交作业,不要漏交
- 不懂的多问问别人
如何获得$>80$的分数
- 默写书本中每一个定理的证明
- Chap.3 之后所有的课后习题刷一遍
- 历年试卷自己带着思考做一遍
上课要求
多问,不懂就问。
符号不明白?问!
某一步别人都懂了就我没懂,我不好意思提?问!
随时打断问!
弱小和无知都不是生存的障碍,傲慢才是
参考书目
苏德矿的书太难了,我实在看不下去怎么办?
- 普林斯顿微积分读本(The calculus life saver)
- 托马斯微积分
Chap .3
费马定理
费马定理是高中知识,它是寻找极值点的重要工具,它给出了一个函数取到极值的条件,也是所有中值定理的基石。它的叙述如下: \(f(x)在x处取得极值,如果f(x_0)的左导数和右导数存在,那么f'(x_0)=0\) 费马证明需要用$(\epsilon,\delta)$数学分析语言,因此一般不作要求。
罗尔定理
罗尔定理是费马定理的一个非常自然的推论,它是说,如果在闭区间$[a,b]$上连续,且在开区间$(a,b)$上可导的函数在区间两端取相同的值$f(a)=f(b)$,那么$f(x)$在$[a,b]$内一定有极值点$x_0,a<x_0<b$,满足$f’(x_0)=0$
罗尔定理的证明是一件很显然的事情,首先闭区间上的连续函数必定有最大值最小值,如果最大值最小值同时在端点处取得,同时端点值又相等,那么函数$f(x)$在$[a,b]$上就是一条直线,显然处处$f’(x)=0$,如果最大值最小值有一个不在端点,那么由费马定理就可以自然推出结果。
罗尔定理的直观
想象你正开车沿着高速公路行驶. 我看到你在一家加油站停了下来. 然后你继续前行, 始终没有改变方向, 虽然你随时可以掉转方向. 过了一段时间, 我又在这家加油站看见了你, 但我不曾跟着你, 看你在这段时间里都做了什么. 我断定:在我不曾跟着看你的某个时刻, 你的车速为零.
为什么我会有信心这样说?其实, 有可能你从来就没有离开过加油站, 这样的话, 你的速度一直为零. 而如果你确实离开过加油站, 并往前开, 那你最终必定在某处掉了头, 否则你不可能又回到加油站. 那么当你停止前进开始掉头时会发生什么呢?你必定停下来过, 哪怕只是一瞬间! 你不可能掉转方向而不让车停下来. 这同抛球运动的情况相似. 在球到达最高点的这一瞬间, 它的速度为零.
另一方面, 你还有可能曾离开加油站, 并倒着开. 在这种情况下, 你也必定曾在某个时刻将挡位由后退改为前进, 而结果是相同的:你在某处停下来过. 无论你向哪个方向走, 你都可能停下来过很多次; 但我知道你至少停下来过一次. 这就是罗尔定理所讲的内容.
拉格朗日定理
拉格朗日定理的直观
想象你开始了另一段旅行, 我发现你在两个小时之内行驶了 100 英里. 因此, 你的平均速度为 50 英里/小时. 这并不是说你在整个行驶过程中速度始终维持在恰好 50 英里/小时. 现在, 我的问题是:你的速度曾经达到过 50 英里/小时吗?哪怕只是一瞬间.
答案是肯定的. 即使你在开始的第一个小时速度为 45 英里/小时, 第二小时为 55 英里/小时, 你仍然不得不从低速加速到高速. 而在这个过程中, 你有一瞬间的速度会是 50 英里/小时. 这是不可避免的! 不管你整个的行驶过程是怎样的, 如果你的平均速度为 50 英里/小时, 那么你会有至少一次瞬时速度为 50 英里/小时.4 当然, 你可能达到 50 英里/小时不止一次 —— 可能很多次, 甚至你能始终以 50 英里/小时的匀速行进. 这就引出了中值定理.
拉格朗日定理的证明
拉格朗日定理的证明是罗尔定理经过一点变化下的推论,它的证明技巧主要是把函数的零点化为函数导数的零点,并通过构造首尾两端相等的函数,用罗尔定理得到零点。
\[\exist \xi \in (a,b),\frac{f(b)-f(a)}{b-a}=f'(\xi)\]它等价于
\[\exist \xi \in (a,b),f(b)-f(a)-(b-a)f'(\xi)=0\]等价于证明
\[\exist \xi \in (a,b),F'(\xi)=0,F(x)=(f(b)-f(a))x-(b-a)f(x)\]只需要证明$F(b)=F(a)$即可
这种证明方式可以用到一道习题中,即p 132页18题,大家可以做一下,然后可以总结一下这种题目有什么类型
Tips:
(1) 需要用反证法,构造矛盾证明如果$\exist t\in(a,b),g(t)=0$,那么$\exist \xi\in(a,b),g’’(\xi)=0$
(2) $[f(x)g’(x)-f’(x)g(x)]’$
柯西定理
柯西定理是拉格朗日定理的推论,它研究的是对于$x$轴施加连续的扭曲(distort)后,新的坐标轴下是否有类似于拉格朗日中值定理的推断
我们证明留作一个习题,但是我们要分析一下其中的一个错误证明方法
这种证明方式用到的典型习题是p131 7题,这一类习题的类型是分母不能写成典型的$b-a$形式,这就是我们所说的”施加了连续变化”
-
Must Know Tips/Tricks in Deep Neural Networks阅读笔记
- 企业级联邦学习——新算法、新范式与未来展望 [ICML2021 Talk]
- 深度神经网络中的持续学习 [ICML2021 Tutorial]
- 隐私保护的深度学习系统——基于高斯机制的差分隐私DL
- PPT分享——满足隐私保护的去中心化无监督域适应范式
- 满足隐私保护的去中心化无监督域适应范式——KD3A [ICML2021]
- An Introduction to the Differential Privacy
- A Literature Survey on Mixup-based Methods
- A Literature Survey on Domain Generalization
- Reproducing Kernel Hilbert Space in Domain Adaptation
- A Brief Introduction of Domain Adaptation