Welcome to FengHZ's Blog!
-
Some useful tricks in training variational autoencoder
简介
训练变分自编码器(Variational AutoEncoder, VAE)并不是一件容易的事情,在VAE非常Fancy的模型背后,其训练过程非常不稳定。在本文中,笔者回顾自己在LIDC-IDRI以及MNIST数据集上的训练经验,给出一些训练的技巧,它们包括:
- VAE损失函数正则化参数的设置与主次矛盾分析
- 损失函数在
pytorch中的写法与学习率设置 - 特征空间维数设置
- VAE结果可视化技巧
-
Some notes on variational inference
变分是什么
微积分是研究函数的手法,它研究在某一个特定函数上的微小变化。而变分则是研究泛函的手段,它通过研究函数的变化,来找到一类将函数映射到实数的泛函的极值点。这里泛函一般被表达为函数以及它们的导数的定积分(将函数映射到实数值)。最大化或者最小化一类泛函的函数往往可以用欧拉-拉格朗日方程来找到。
-
Rethinking ImageNet Pretraining
前言
本文是何凯明在
FAIR的新作,主要针对使用ImageNet进行预训练的问题。一直以来,在计算机视觉任务上,采用ImageNet数据集对设计好的神经网络进行预训练,然后再用目标数据集对神经网络进行训练是一套标准的流程,而很多在标准数据集上达到
State of Art的结果也沿用了这一套训练模式。但是,预训练到底起到了多大的结果呢?它是否有助于最后训练结果的提升呢?本文主要给出了这个问题的量化。
-
An introduction to Variational Autoencoders-Background,Loss function and Application
前言
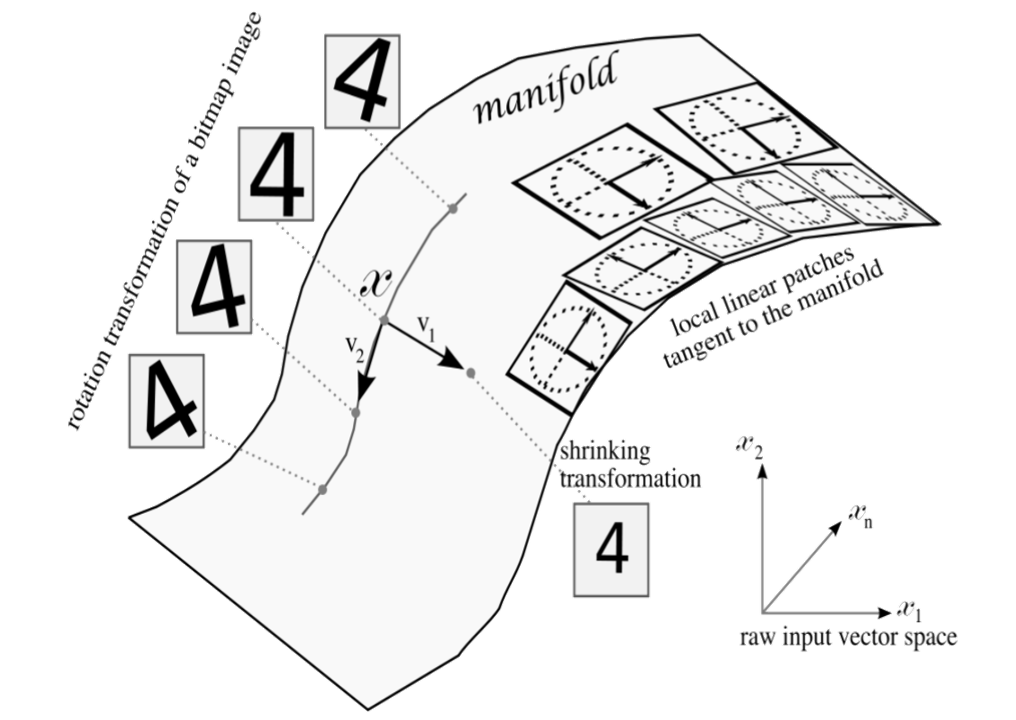
Variational autoencoders(VAE)是一类生成模型,它将深度学习与统计推断相结合,可用于学习高维数据$X$的低维表示$z$。与传统自编码器不同,Variational autoencoders 假设$X$与$z$都是满足某种分布假设的随机变量(向量),因此Variational autoencoder 本质是对随机向量分布参数的估计(如均值,方差等矩估计)。在这个假设下,我们可以利用分布函数假设与预测参数对$p(X\vert z)$与$p(z\vert X)$进行估计,用最大似然设计损失函数,并利用概率分布$p(X\vert z)$来对$X$进行采样与生成。
本文旨在对VAE进行基于背景,损失函数以及应用方面的介绍。本文先对VAE所需要的数学知识与基本假设进行简要描述。同时,在写作本文主体部分过程中,本文主要以Tutorial on Variational Autoencoders为主干进行翻译工作,并辅以其它参考资料对该文献的观点进行选择性删减,重整理与补充性叙述,同时对该文章中省略或笔者认为叙述不清数学证明与显然性描述进行补全与解释。为了对照方便起见,本文自第二部分起,主要结构与该文献结构一致,读者可以自行选择直接阅读本文,或者阅读该文献并辅以本文进行辅助理解。
本文写作过程中主要参考资料为:
-
A paper report for paper - Unsupervised Feature Learning via Non-Parametric Instance Discrimination
简介
Unsupervised Feature Learning via Non-Parametric Instance Discrimination是CVPR2018的一篇无监督特征提取方法,且是一篇Oral文章。它采用实例区分(Instance Discrimination)构造实例分类器对图像进行无监督特征提取,所提取的特征可以很好地用于图像的相似度度量任务中。
我为此文撰写了一个report进行深度分析,report以slice形式进行呈现。论文中为了解决实例分类器类别不均衡的问题采用了Noise Contrastive Estimation方法,该方法的数学推导我放于Applendix中。
-
A paper report for paper - dynamic routing between capsules
简介
Dynamic Routing Between Capsules是Hinton于2017年11月所撰写的一篇关于神经网络设计架构的文章。文章的主要观点是Vectorization,即用向量代替标量来表示特征,同时用向量的范数来代替分类可能性,向量之间的连结用动态路径进行连结。
我为此文撰写了一个report进行深度分析,report以slice形式进行呈现。
-
A mind map for paper - a survey on deep learning in medical image analysis
简介
本文提供了一个思维导图用来归纳2017年中旬发表的关于深度学习应用于医学影像分析情况的一篇综述A survey on deep learning in medical image analysis。综述分5部分进行叙述,第一部分介绍了医学影像分析研究从专家系统到深度学习技术的发展历史,第二部分综述了已用于医学影像分析的深度学习技术与模型结构,第三部分描述了具体应用深度学习技术的医学影像分析领域(分类任务,检测任务,分割任务,配准任务,图像检索任务,图像生成与图像增强任务),第四部分描述了深度学习技术得到成功应用的解剖组织结构,如神经元组织,视网膜等,并描述了每一个具体解剖组织所需要解决的问题,第五部分归纳了深度学习成功应用的重点,阐述了深度学习在医学影像分析中面临的挑战,并总结了未来研究热点。
我将以思维导图的形式给出本文的直观描绘,导图以文章小节作为节点,并概括描述了每一个节点下的主要内容与重点。
-
A tutorial of Kullback-Leibler divergence
参考资料:Jon Shlens’ tutorial on Kullback–Leibler divergence and likelihood theory
FengHZ’s Blog 首发原创
笔记大纲
KL散度(Kullback-Leibler divergence)是用来度量两个概率分布相似度的指标,它作为经典损失函数被广泛地用于聚类分析与参数估计等机器学习任务中.
本文将从以下几个角度对KL散度进行介绍:
- KL散度的定义与基本性质
- 从采样角度出发对KL散度进行直观解释
- KL散度的应用以及常见分布KL散度的计算
-
A tutorial on spectral clustering文献翻译
论文题目: A tutorial on spectral clustering
前言
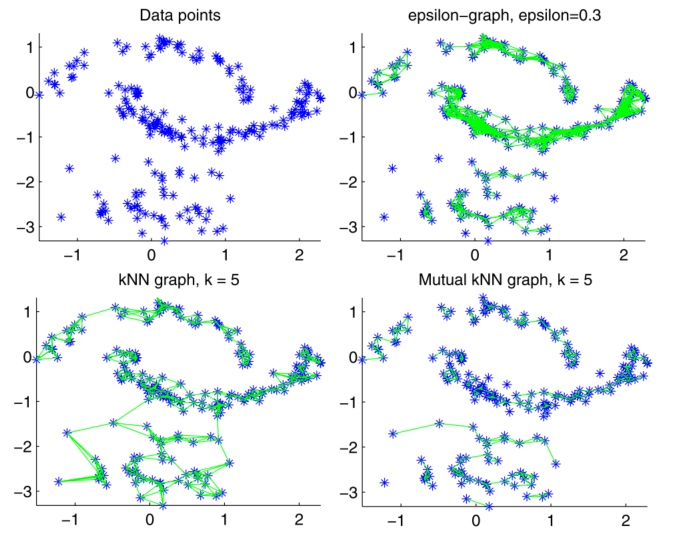
谱聚类是一类很前沿的聚类算法,它的特点是具有极强的可解释性。这篇文章不仅从根源上深入浅出介绍了谱聚类与其算法,同时使用图割理论,随机游走理论(用Markov状态转移矩阵作为工具)以及矩阵扰动理论从不同角度剖析了谱聚类的直观意义以及我们如何使用谱聚类。在看整篇论文的过程中,我不断被这些直观简洁的解释所吸引,并为此文作者的迷人思想所折服.这就是促使我翻译这篇文章的原因。
因为时间所限,我暂时翻译了第1-5章节,这些章节主要介绍了谱聚类与如何做谱聚类,并为谱聚类给出了一个与图割问题的线性规划松弛解的等价性证明,以及第8章节,主要是关于如何使用谱聚类,如何选择超参数与正确的拉普拉斯图矩阵的问题.我会在未来翻译第6章节,一个关于谱聚类问题的随机游走理论与马尔科夫链的平稳状态分布解以及第7章节,用矩阵扰动理论解释谱聚类.第9章节是一些扩展性内容与文献推荐,此处暂时不翻译。
以下是翻译部分
-
一个对优化算法等价于滑动平均的思考
题目:一个关于优化算法等价于时间序列的思考
FengHZ‘s Blog首发原创
起因
Tensorflow官网上有一个Trick是这样的:
当训练参数到一定的步数之后,可以考虑采用 \(\hat{w_t}=mw_{t}+(1-m)w_{t-1}\) 来让参数收敛到一个更好的效果,但是这个有时候会有作用,有时候并没有作用
我觉得这个策略等价于调整momentum与学习率,特此给出证明与分析
- 企业级联邦学习——新算法、新范式与未来展望 [ICML2021 Talk]
- 深度神经网络中的持续学习 [ICML2021 Tutorial]
- 隐私保护的深度学习系统——基于高斯机制的差分隐私DL
- PPT分享——满足隐私保护的去中心化无监督域适应范式
- 满足隐私保护的去中心化无监督域适应范式——KD3A [ICML2021]
- An Introduction to the Differential Privacy
- A Literature Survey on Mixup-based Methods
- A Literature Survey on Domain Generalization
- Reproducing Kernel Hilbert Space in Domain Adaptation
- A Brief Introduction of Domain Adaptation