FengHZ‘s Blog首发原创
Recently, Vector-Quantization based generative models have raised great attention these days. The model VQ-VAE2 gives the most clear and realistic generation of images among all autoencoder models with quality that rivals the state of the art result of BigGAN.
In this article, I wanna to give a brief summary of the main ideas for the 2 articles.
Vector Quantization
We have illustrated the main idea of vector quantization in this article. If we want to compress a batch of image(with K bits each pixel) into M bits, we can do k-means for all the 3-d vectors in this image batch, allocate the class label for each vector and generate a M-vector Cookbook for the batch. In de-compress progress, We just need to fill the class label with related 3-d vector in the M-vector Cookbook.
A natural thought is that if we can do vector quantization in the raw image space, we can also do it in the low-dimensional latent space. The two paper VQ-VAE & VQ-VAE2 are all based on this thought.
VQ-VAE
Basic Assumption
The basic assumption of VQ-VAE extend the latent variable assumption to latent vector. To be brief, as shown in the following figure, we assume each image can be generated from a low-dimensional structured latent space $\mathcal{S}$ with k basises which form a so-called cookbook.
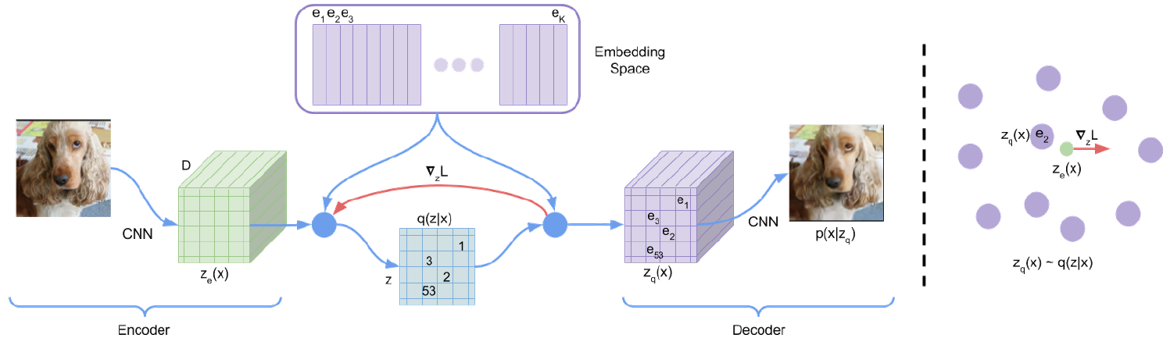
In encode progress, we map the high-dimensional latent representation $z_{e}(x)$ into $\mathcal{S}$ utilizing k nearest neighbour algorithm. In decode progress, we firstly reconstruct $z_{e}(x)$ with the basises in cookbook and form the compressed high-dimensional representation $z_{q}(x)$. Then we use $z_{q}(x)$ as decoder input and reconstruction the raw image x.
Implementation Details
With the brief and simple idea, how to make it work is very important. There are 3 main problems in the implementation process
-
How to form the cookbook with the random initialization
-
How to calculate the gradients of the transform from $z_{e}(x)$ to $z_{q}(x)$
-
How to process the relation ship between the $z_{e}(x)$ and the related basis.
The paper VQ-VAE proposes a loss function to deal with 1 and 3. Here we use $D,E$ to represent decoder and encoder and use $sg$ to represent stop gradient operation.
\[\mathcal{L} = \Vert x-D(z_{q}(x)) \Vert_2^2 + \Vert sg(z_{e}(x)) - z_{q}(x)\Vert_2^2 + \beta \Vert z_{e}(x)-sg(z_{q}(x))\Vert_2^2 \tag{1}\]And the gradients of the transform from $z_{e}(x)$ to $z_{q}(x)$ can be approximated as equal
\[\nabla_{z_{e}(x)}\Vert x-D(z_{q}(x)) \Vert_2^2 = \nabla_{z_{q}(x)}\Vert x-D(z_{q}(x)) \Vert_2^2 \tag{2}\]$(1)$ is very easy to understand. If $\Vert z_{e}(x) - z_{q}(x)\Vert_2^2=0$, then we precisely map the input space into one permutation of the basises in cookbook.
$(2)$ is an approximation work well in implementation. In the ideal situation, the transform should be identity map so we get $(2)$. To make $(2)$ more reasonable, the author propose $(3)$ as the update for cookbook
\[N_{i}^{(t)} = N_{i}^{(t-1)} * \gamma + n_{i}^{(t)}*(1-\gamma) \\ m_{i}^{(t)} = m_{i}^{(t-1)} * \gamma +(1-\gamma)*\sum_{j}^{n_{i}^{(t)}} z_{e}^{(t)}(x)_{i,j}\\ e_{i}^{(t)} = \frac{m_{i}^{(t)}}{N_{i}^{(t)}} \tag{3}\]Here $n_{i}^{(t)}$ means the number of the vectors in $z_{e}^{(t)}(x)$ represented by the $i-th$ cookbook vector in kNN algorithm.
VQ-VAE2
VQ-VAE2 has 3 main contributions:
-
Extend the VQ-VAE model to ImageNet
-
Propose a hierarchical structure for VQ-VAE
-
Use pixel-cnn to do generation in the structured latent space, which takes the discrete quantization result $q(z\vert x)$ as inputs and the reconstruction target.
Hierarchical Structure
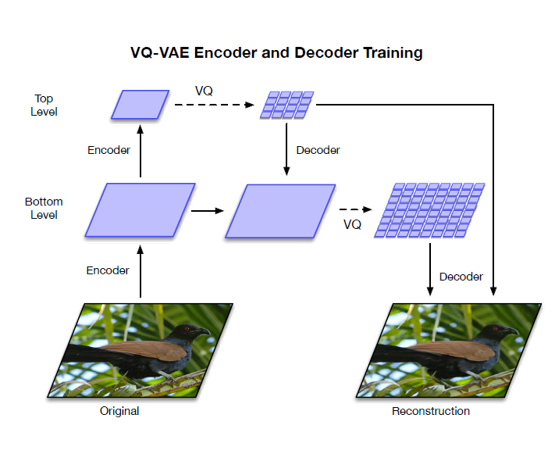
The hiearachical structure itself really has nothing new. As we mentioned in hierarchical vae, it just combine the local and global information.
Pixel-CNN as generation for $q(z\vert x)$
Pixel-CNN models utilize autoregressive method to generate image pixel-by-pixel. Given enough calculation resource and enough time, we can generate results with good quality. However, the pixel-by-pixel generation process is very counterintuitive and time-comsuming, which limits the usage in large size images. However, if we take the quantization result $q(z\vert x)$ as the object for pixel-cnn, it will achieve a good balance between generation quality and run time.
The author trains a pixel-cnn++ to reconstruction and sample $q(z\vert x)$, just as the following schematic diagram illustrates

Todo List
The details of pixel-cnn