FengHZ‘s Blog首发原创
“Top-1 Error”, “Top-5 Error”, “mean AP”, “ROC”, “AUC”, 分类任务中常常可见这些度量方法。同时, 从二分类问题到多分类问题再到几千分类问题, 随着问题规模的扩大, 不同的分类准则也不断涌现。本文旨在对这些分类指标做一个从历史, 原理到计算方法与可用计算函数之间的梳理, 以方便查阅。
本文主要参考资料为:
定义数据集为 $\mathcal{D}=(x_1,\ldots,x_N)$, 同时记我们对数据集中每个数据的预测得分为$\mathcal{S}=(y_{1}^{s},\ldots,y_{N}^{s})$,以某个s为阈值(高于s的分类为positive,小于等于s的分类为negative)我们可以将$\mathcal{S}$映射到一个具体的one-hot预测$\mathcal{P}=(y_{1}^{p},\ldots,y_{N}^{p})$, 其真实标签为 $\mathcal{G}=(y_{1}^{g},\ldots,y_{N}^{g})$.
Basic Index
我们对基本二分类问题定义一些分类的基础指标：
-
True Positive(TP), True Negative(TN), False Positive(FP), False Negative(FN)
TP,TN,FP,FN可以看成是依据以下规则将$\mathcal{D}$划分成的4个集合
- 我们说一个样本$i$的预测是属于TP的，当且仅当 $y_{i}^{p}=y_{i}^{g}=1$
- 我们说一个样本$i$的预测是属于TN的，当且仅当 $y_{i}^{p}=y_{i}^{g}=0$
- 我们说一个样本$i$的预测是属于FP的，当且仅当 $y_{i}^{p}=1,y_{i}^{g}=0$
- 我们说一个样本$i$的预测是属于FN的，当且仅当 $y_{i}^{p}=0,y_{i}^{g}=1$
-
混肴矩阵与衍生指标
基于1中的4类基础指标，我们给出混肴矩阵如下
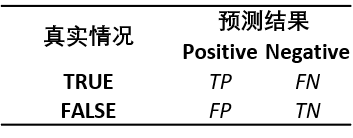
通过混肴矩阵的排列，我们给出以下几种有意义的指标
- Precision
- Recall
- Accuracy
- True Positive Rate(Recall)
- True Positive Rate
关于几种扩展指标的解释
Precision针对于分类器预测为Positive的集合，主要看分类器对正类预测的准确度。Precision过小，说明我们对Positive的预测出了很大的问题，分类器倾向于把很多实际为False类的样本归于Positive类。如果一个分类器致力于提高Precision，那么一个很简单的做法就是只把置信度很高的样本归类于True。以深度学习分类任务为例，我们只把预测出score很高的(比如0.9以上的)归类为Positive，这样自然预测的Positive的质量会很高，但是会导致Recall的降低。对Precision的理解可以表示为”宁可放过1000，绝不错杀一个”。
Recall针对于实际上是True标签的集合，主要看分类器对于实际上是True标签的样本预测的准确度。如果一个分类器致力于提高Recall，说明这个分类器对能不能找到True标签的样本看的很重。以深度学习分类任务为例，我们把归类为Positive的阈值score调低，(比如0.1以上的归类为Positive)，就可以让Recall增加。对Recall的理解可以表示为”宁可错杀1000，绝不放过一个。”
因此，Precision与Recall本质上是对分类阈值的两种限制。在给定分类结果以后，如何选择一个合适的阈值使得Precision与Recall都比较合适呢？这就引出了PR曲线。PR曲线就是一个对已有预测结果的score范围进行穷取，然后绘制曲线的过程，它的计算方法如下：
-
按$y^s$(也就是score,$\mathcal{S}$)从大到小的序列对$y^s$以及对应的$y^g$排序，一个例子如下
-
按排序过的$y^s$的取值分别由大到小设置分类阈值$s_i$，对每一个$s_i$，可以将$y^s$映射到一个one-hot预测分布。比如此时我们取$s=0.89$，则一个对one-hot编码映射为
此时可以计算$s_i$所对应的一组$(\text{recall}_i,\text{precision}_i)$
-
将$(\text{recall}_i,\text{precision}_i)$描在坐标轴上，横轴为recall，纵轴为precision。不同点之间用直线连接，一个样例如下
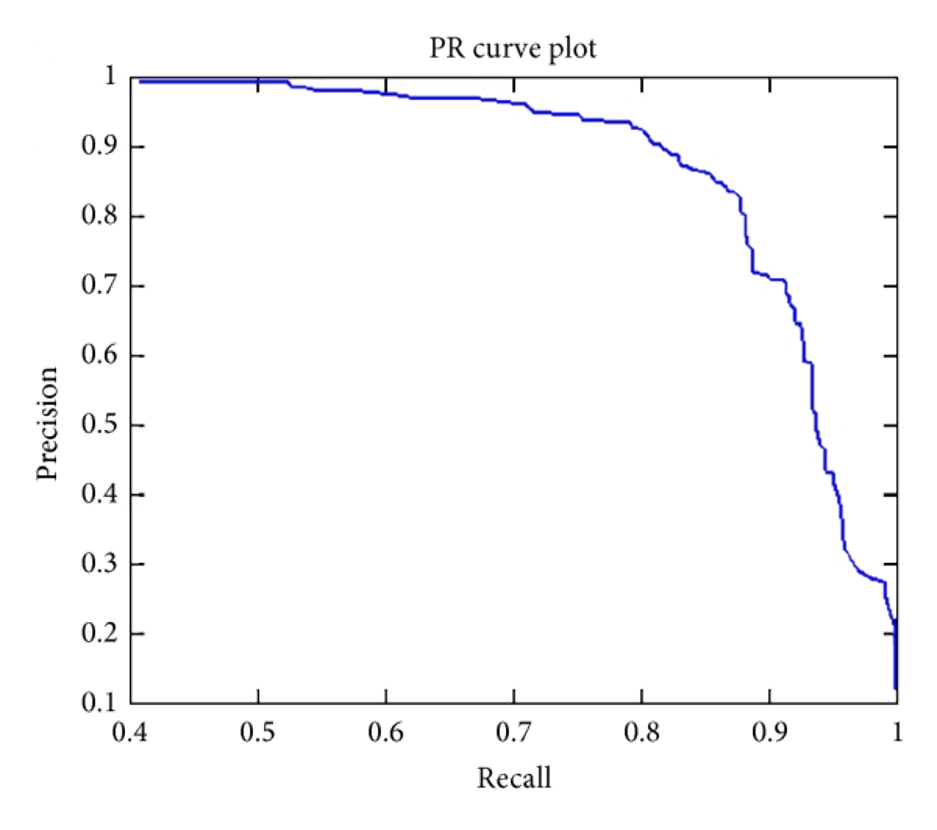这种曲线我们称为P-R曲线。如果分类器A的P-R曲线被分类器B完全包住，说明相同查准率下B的查全率比A高，相同查全率下B的查准率比A高，则分类器B优于分类器A。同时，我们还可以根据precision=recall，或者基于precision与recall的权值给定价值函数并找到最优score。
我们还可以用一些损失函数，如
\[\text{F1} = \frac{2*\text{precision}*\text{recall}}{\text{precision}+\text{recall}}\]来找到最优点。
注意到我们又引入了一个新指标FPR，它与recall相反，它针对实际标签是False的集合，主要看分类器对于实际上是False标签的样本预测的准确度。如果一个分类器的FPR较高，那么说明在所有标签为False的样本中，分类器把它判断为Positive的概率比较大。同样以深度学习任务为例，我们同样也可以把归类为Positive的阈值score调高，(比如0.1以上的归类为Positive)，我们固然会增加precision(即模型预测Positive的质量增加了)，但是对Negative预测质量降低了，即将score调低，那么FPR也会变得很高。因此，对同一个score而言，FPR与Recall的单调性刚好相同，score越低，FPR越高，Recall也会越高，score为0的时候(所有样本都预测为Negative)，这个时候FPR达到最高(此时所有样本都预测为正例，FPR=1)，而Recall则肯定为1。但是注意到，对于一个完美的分类器，它应当满足所有标签为True的样本的得分应该比标签为False的样本高，也就是说，在这个完美的分类器下，会经过这样一个过程:
一开始取score较大的时候，TPR一直为0，但是Recall在增长，即Recall在 x=0这一直线上向上爬升直到(0,1)点。然后慢慢地，随着score减小，TPR增大直到所有样本都预测为正，此时TPR为1，而Recall则永远不变为1。即一个完美分类器的曲线应该是(0,0)-(0,1)-(1,1)这样的曲线。
因此，与P-R curve一样，我们可以绘制ROC曲线，并希望该曲线逼近完美分类器曲线。我们希望这个曲线在Recall较大的时候，(开始放水的时候)TRP也不至于太大，最好满足 Recall=1,TPR=0，ROC曲线中一个曲线包裹另外一个曲线，也可以说明一个分类器优越于另外一个。
ROC曲线可以如P-R曲线一样绘制，一个典型的例子如下图所示：
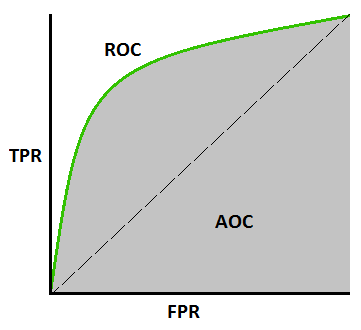
我们可以计算曲线下面积作为评价标准，该评价标准称为 AUC(Area Under Curve)
对多分类的推广
前面所述都是针对二分类问题而言，对于C分类问题，我们可以将其转换为C个二分类问题，并采用平均法来进行。假设我们对C个二分类问题，对于第i个阈值点全部计算了
\[(\vert \text{TP} \vert_{i}^{c},\vert \text{TN} \vert_{i}^{c},\vert \text{FP} \vert_{i}^{c},\vert \text{FN} \vert_{i}^{c}), i = 1,\ldots,N,c=1,\ldots,C\]我们可以用macro-Recall,macro-Precision,macro-FPR来计算C个类的广义平均，也可以用micro-Recall,micro-Precision,micro-FPR来计算C个类的狭义平均
\[\text{macro-Recall} = \frac{1}{N}\sum_{i=1}^{N} \text{Recall}_i \\ \text{macro-Precision} = \frac{1}{N}\sum_{i=1}^{N} \text{Precision}_i \\ \text{macro-FPR} = \frac{1}{N}\sum_{i=1}^{N} \text{FPR}_i \\\]对于micro的计算，只需先计算$\bar{\text{TP}},\bar{\text{TN}},\bar{\text{FP}},\bar{\text{FN}}$，然后再用这些指标各自计算即可。
Accuracy 与 top-5 error
对单标签或多标签计算Accuracy的过程都很简单，就是算一下有多少预测对了的样本再除以总数就好。对于top-5 error而言，即我们对多标签类别进行预测的时候，对最后结果预测5次，每次预测第k高score所对应的类别。只要最终结果出现于5次预测中的任意一次，我们就说其预测是正确的。用该结果除以总数得到 top-5 accuracy，要求得 top-5 error只需1-top-5 accuracy。
AP与mAP
对于二分类任务，我们可以通过计算 AP的方式来得到结果。AP就是Average Precision，即我们如上文一样按照score排序的阈值计算Precision,然后再求平均即可。
mAP针对多分类任务，无非是分别计算二分类任务的AP再求得平均。