FengHZ‘s Blog首发原创
基于标注监督的深度学习技术已经取得了巨大的成功,并极大推动了计算机视觉(CV),自然语言处理(NLP)等领域的进步。一般而言,只要构造一个足够大的数据集,且这个数据集拥有高质量的标注,我们就可以构造模型容量(Capacity)足够大的神经网络,通过反向传播(Back-Propagation)与随机优化算法(SGD,RMSProp,Adam)训练神经网络,并在测试集上达到足够高的泛化性能。但是,获取高质量的数据不是一件容易的事情。深度学习所需要的数据燃料以万计,获得较为精确的标注需要大量的人力,尤其是当数据标注涉及专家知识的时候,获得标注则变得极为昂贵。
半监督学习(semi-supervised learning)正是应对这种情况而生的方法。对于很多任务,获取原始数据成本低廉,而获取标注成本较高。在这些任务上,半监督学习算法可以同时利用少量有标注数据与大量无标注数据进行训练,其结果可以大大提高模型的泛化能力,甚至在某些任务上接近全监督学习的效果。
本文主要介绍半监督学习的发展历史以及现在主流深度半监督学习算法的三个派别:
- 基于深度生成模型的半监督学习算法
- 基于差异学习的半监督学习算法
- 基于图模型的半监督学习算法
其中,每一个派别内都会有许多不同的分支,对于每一个分支我们也将进行细分叙述。因参考文献较多,我们将参考文献放于文末,同时本文会保持持续更新。
半监督学习:历史与发展1
想象一个情景,假如我们有大量无标注数据,同时有少量有标注数据,如何利用无标注数据呢?一个最自然的想法是,我们用有标注数据去训练一个较为简单的模型,用模型对于无标注数据进行预测,然后把那些置信度不高的结果(如预测概率在0.5附近的模型)挑出来,对这些结果打上标注,再训练一个稍微复杂一些的模型。如此反复直到模型取得最优效果。这种方法称为”主动学习”(Active Learning),其目的是使用尽量少的”查询”(query)来获得尽量好的性能。
主动学习引入了额外的专家知识,同时通过与外界的交互将部分未标记样本转化为有标记样本,它是一种间接的半监督学习方法。能否在不引入新专家知识的情况下,用未标记样本提高泛化性能呢?在一些假设的情况下,答案是可以的。通过以下四种不同的假设,我们可以得到四个半监督学习算法的一般范式(paradigm).
-
未标记数据与标记数据来源于同一数据分布,数据分布存在潜变量模型假设,在潜变量空间内存在簇状聚类结构,同一个簇的数据属于同一类别
在该假设下,我们可以用生成模型进行半监督学习。给定有标注样本集
\[D_{l}=\{(x_1,y_1),\ldots,(x_l,y_l)\}\]以及无标注样本集
\[D_{u}=\{x_{l+1},\ldots,x_{l+u}\}\]同时假设所有样本独立同分布,对应的生成模型为$\mathcal{G}$, 生成潜变量分布为 $z_i\sim \mathcal{N}(\mu_i,\Sigma_i)$, 那么 我们可以最大化 $D_{l}\cup D_{u}$的对数似然
\[LL(D_{l}\cup D_{u}) = \sum_{(x_j,y_j)\in D_{l}} \ln p(x_j,y_j\vert z_j) +\sum_{x_j\in D_{u}}\ln p(x_j \vert z_j)\]生成模型将标注看成是潜变量之一,在有标注的时候将其视作已知潜变量进行生成,在无标注的时候利用生成模型的自监督损失函数进行自动拟合。一般而言,数据越多,对统计量的预测也就越准确,生成模型表现也就越好。我们利用大量数据去拟合一个优秀的生成模型,将标注看成是低维空间的潜变量,采用少量有标注样本引导模型学习这种潜变量,从而完成半监督学习。
-
未标记数据与标记数据来源于同一数据分布,彼此相似的数据有很高的可能性属于同一类别
该假设是基于图的半监督学习方法的基本假设。基于图的半监督学习方法需要先用无监督方法学习(或定义)一个近邻矩阵(Affinity Matrix) W, 其中$W_{i,j}$表示第i个样本与第j个样本的相似度. 依据我们的假设直观,模型对于相似样本的预测也应该是相近的,定义模型对样本x的预测为 $f(x)$, 我们可以定义模型在近邻矩阵W下的能量函数
\[E(f) = \frac{1}{2} \sum_{i=1}^{m}\sum_{j=1}^{m}W_{i,j}(f(x_i)-f(x_j))^2=f^TLf \tag{1}\]其中$f=(f(x_1),\ldots,f(x_m))^T$,L为W的Laplacian矩阵.
对于有标注的数据,我们给定约束$f(x_l)=y_l$, 并将其代入$(1)$. 对于无标注数据,我们要求其在$(1)$下达到最小能量函数,并对$f$进行优化. 优化问题可以转化为一个图割问题解决.
-
未标记数据与标记数据来源于同一数据分布,不同标签数据的划分边界是低密度的。
在该类假设下,分类器试图找到将有标记样本划分开,同时划分区域穿过数据低密度区域的划分超平面。此时,未标记数据起到了揭示数据聚类结构的作用,如下图所示。
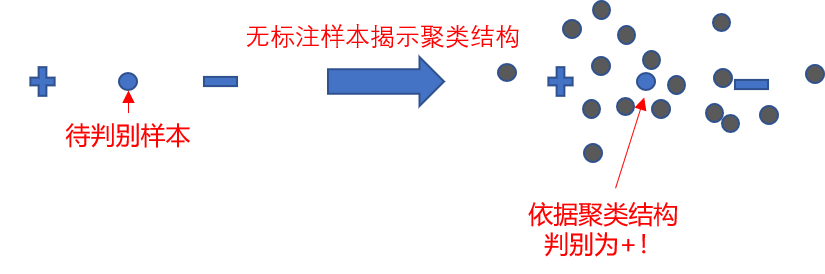
半监督SVM算法是一种利用低密度划分的半监督学习算法。
-
未标记数据与标记数据的源数据具有多个视图,不同视图对应的标记空间相似
在该类假设下,一个数据由多个视图组成,不同视图对应的标注空间相同,我们可以利用多视图的”相容互补性”,通过协同训练来进行半监督学习:首先在每个视图上基于有标记样本训练分类器,让每个分类器挑选自己最有把握的样本赋予伪标记,将伪标记提供给其他视图的分类器作为新增样本重新训练,这种”互相学习,共同进步”的过程不断迭代进行,直到分类器不再发生变化。
协同训练可以推广到单视图,通过构造不同的学习算法,或者不同的数据采样,甚至是不同的参数设置产生不同的学习器,利用学习器之间的”分歧”相互提供伪标记样本提升泛化性,因此这种方法范式也被称为”基于差异的半监督学习方法”.
对半监督学习方法的评价有两种模式,一是纯半监督学习,二是直推学习。纯半监督学习是指直接预测测试集的数据作为最后的结果,而直推学习则是指预测用于训练的未标注数据,将该预测值作为训练结果。如果用于训练的未标注数据的预测结果较为优秀,则说明模型确实利用到了未标注数据来改进目标预测结果,如果测试集数据的预测结果较好,则说明模型利用未标注数据提高了泛化性。
半监督学习的研究一般始于地球科学与遥感领域,第一篇与半监督学习相关的文章发表于 IEEE Trans on Geoscience and Remote Sensing, 题目为 “The effect of unlabeled samples in reducing the small sample size problem and mitigating the Hughes phenomenon.” 在二十一世纪初,随着现实中对未标注数据利用的重大需求涌现,半监督算法蓬勃发展。从2008年以来,在每年ICML大会所评选的十年最佳论文中,半监督学习的四大范形中的三篇代表论文均获奖。现今的深度半监督方法仍属于以上四个范式,但是深度学习的加入使得模型的泛化能力提升了一个层次。
基于深度生成模型的半监督学习算法
深度生成模型发展到现在有三个派别,它们分别是对抗生成网络(GAN[2]), 变分自编码器(VAE[3]), 以及自回归像素生成网络(PixelCNN,PixelRNN[4]), 由于自回归生成网络训练速度较慢, 深度半监督学习常用前两者作为基本生成模型.
Semi-supervised GAN
基于对抗生成网络的半监督学习的基本思想非常简单,即将二分类判别器修改为C+1分类判别器, 损失函数要求来源于真实数据分布的输入被分为前C类,而生成器生成的数据则被分为C+1类,同时在训练判别器时要求将输入的有标签数据进行正确分类. 文献[7]指出训练出好的半监督结果与好的生成模型不可兼得,并给出了用GAN做半监督的最好结果(14.41% in Cifar10 and 4.25% in SVHN).
Semi-supervised VAE
变分自编码器构建了一个由生成过程和推断过程两部分构成的概率模型,分别由参数 $\theta$ 和参数 $\phi$ 表示。概率模型基于潜变量假设,用于推断连续潜变量$z$与离散潜变量$c$的概率分布。模型对$z$与$c$分别作出了假设
\[p(z) = \mathcal{N} ( z ; 0, I);\qquad p(c)=\text{Mult}(c;K,\pi);\qquad p_{\theta}(X\vert z,c)=f(X;z,c,\theta)\]并利用证据下界(ELBO)得到$q_{\phi}(z\vert X),q_{\phi}(c\vert X)$来对潜变量的后验分布$p(z\vert X),p(c\vert X)$进行近似推断如下
\[\log p(X) \geq E_{q_{\phi}(z,c\vert X)} [\log p_{\theta}(X\vert z,c)]-\text{KL} ( q_{\phi}(z\vert X) \Vert p(z))-\text{KL} ( q_{\phi}(c\vert X) \Vert p(c) )=\text{ELBO}\]在半监督变分自编码器中[13],我们将标签$y$视作离散潜变量$c$的真实后验分布$ p(c\vert X)=\text{Mult}(c;K,y)$,对于有标签的数据,将$y$代入固定采样,对于无标注的数据,我们采用无监督训练来对标签进行推断。同时,该文献发现,单纯用上述训练过程无法有效利用标签,因此其在训练有标注数据时额外增加了一项交叉熵,即
\[-\text{ELBO}-\log q_{\phi}(y\vert X)\]值得注意的是,虽然半监督VAE的假设和理论更加符合数学直觉,但是半监督VAE的效果一直很差,同时,为什么要增加交叉熵项也没有很好的解释。今年一篇文章针对这两个问题对VAE进行了改进,它通过一个近似等式,得出了交叉熵项实际上可以通过ELBO的形式通过一个近似所自然给出,同时结合VAE方法与下文中的Mixup方法提出了OSPOT-VAE,将VAE在半监督数据集上的表现进行了极大的增强,给出了利用VAE做半监督最好的结果(6.11\% in Cifar10, 25.30\% in Cifar100), 可惜被ICLR拒了。
基于差异学习的半监督学习算法
深度半监督学习算法的另外一个套路是人为制造我们不想看到的差异,并对差异施加正则化约束从而让网络在训练过程中减小该差异,并证明这种差异学习可以提高网络在(纯)半监督学习任务上的泛化性能。
Data Augmentation Based Method
数据增广是一种增加泛化性, 避免过拟合的手段. 我们可以通过对无标注数据$\mathcal{D}_u$采样数据增广方法AutoAugment构造差异性, 并通过消除预测差异性来进行半监督学习, 其构造的半监督损失函数如下
\[L_{u} = \sum _{x',x''\sim AutoAugment(x)}\Vert f(x')-f(x'')\Vert_2^2\]数据增广有不同的方法,我们可以直接进行数据增广,也可以采用Dropout进行等价增广,甚至可以采用Mixup方法进行线性增广.
Direct Unsupervised Data Augmentation.
基于减少数据增广差异的半监督学习策略依赖于数据增广方式选择, 文献[5]采用的数据增广策略取得了最好的结果(Cifar10 from 7.66% to 5.27%). 该数据增广策略是用强化学习对各个数据集学出的最佳策略, 我们已经在Data Augmentation 一文中做了详细介绍(这里吐槽一下谷歌真是家大业大, 前面用350块GPU做NAS, 这里用300块GPU做Data Augmentation的强化学习).
文献[5]还针对有标注与无标注数据标注量不均衡时提出了缓解模型对有标注数据过拟合的方法. 简单而言, 就是在每一轮训练时设置一个置信度阈值, 对于有标注数据的预测值高于该阈值的数据计算损失的权重设置为0, 这样可以避免在那些已经分类正确的样本上过份拟合。文中提出了基于指数的置信度设置方法
\[\eta(\text{epoch})=\text{exp}(-5*(1-\frac{\text{epoch}}{\text{max epoch}}))*(1-\frac{1}{C})+\frac{1}{C}\]其中C代表类别个数.注意到这种权重调整策略也常用作标注样本损失与无标注样本损失之间的平衡系数.
$\Pi$-model
与直接用数据增广法类似, $\Pi$-model[9]结合Dropout与数据增广方法进行差异构造, 这种算法的一个简单伪代码表述如下

同时, 注意到此时产生正则化损失的目标 $z_i,\tilde{z}_i$都会导致梯度计算, 最终使得结果向$\frac{z_i+\tilde{z}_i}{2}$靠拢, 这在具体的工程实践中是有害的(亲测被这个问题坑过很多次), 一个工程上的解决方法是在每一个epoch中固定$\tilde{z}_i$作为不计算梯度的target, 而迫使网络预测逼近 target. 这个思路在之后的诸多半监督学习方法中都有使用, 如后文提到的MixMatch方法采用多次计算取平均来生成target, Mean Teacher方法产生Teacher与Student两个网络来生成Target. $\Pi$-model 同样给出了用滑动平均方法生成target的策略, 即对于样本$x_i$, 在第k个epoch中的target $\tilde{z}_i^{(k)}$ 可以由计算生成的$z_i^{(k)}$以及上一轮所用的 $\tilde{z}_i^{(k-1)}$经过滑动平均生成
\[\tilde{z}_i^{(k)} = \alpha \tilde{z}_i^{(k-1)} + (1-\alpha) z_i^{(k)} \\ \tilde{z}_i^{(k)} = \tilde{z}_i^{(k)}/\text{sum}(\tilde{z}_i^{(k)})\]Mixup Method
Mixup是一种数据增广方法,它通过对输入数据与标签进行成对插值,从而让模型学习到数据之间的连续变化与对应标签的连续变化,提高模型的泛化性。我们已经在这篇post中系统介绍了mixup方法并开源了我们的详细实现代码
Mixup方法可以作为半监督训练中的差异产生器用于提升模型的半监督训练性能,记有标签数据为$\mathcal{D}_l$,无标签数据为$\mathcal{D}_u$, 则算法伪代码如下:
-
Input:
Batch of labeled examples and their one-hot labels
\[(x_b,l_b)\in \mathcal{D}_l;b\in (1,\ldots,B)\]Batch of unlabeled exmaples
\[u_b \in \mathcal{D}_u;b\in (1,\ldots,B)\]Beta distribution parameter $\alpha$ for Mixup, weight $\gamma$ between the supervised loss and mixup loss
Network model f as well as its parameter w
-
for b in 1 to B do:
$xp_b=f(x_b)$
supervised_loss = CrossEntropy($xp_b,l_b$)
$up_b = f(u_b)$
$m_b,mp_b$ = Mixup($u_b,up_b$)
mixup_loss = MSE($f(m_b),mp_b$)
loss = supervised_loss + $\lambda$ * mixup_loss
loss.backward()
update w by gradient
MixMatch
基于Mixup的半监督学习方法已经取得了很出色的成果,在我们的Github实现中,对于Cifar10数据集,仅用10%标注就实现了93.06%的精度, 离全监督的精度仅差3%.
但是, Mixup在半监督学习的应用潜力仍有待于进一步挖掘。2019年5月, 混合了 DataAugmentation 与 Mixup 方法的 MixMatch[6] 刷新了各大半监督学习问题的精度上界,我们在这里特意强调一下这种方法。
简单而言, MixMatch方法在原有的Mixup方法的基础上增加了DataAugmentation操作,使得其对无标注数据的预测更加准确,同时对无标注数据的伪标签$up_b$做了中心化操作,使得预测伪标签更加接近于one-hot编码,信息熵更小。其算法细节如下:

得到$\mathcal{X’,U’}$后, 分别计算CrossEntropy以及MSE即可.
- Augment由7个策略组成, 每次随机挑选策略与参数进行. 7个策略包括左右翻转, 高斯模糊, 对比度正则化, 高斯噪声, 通道随机增强/减弱, 仿射变换.
- 注意到生成$\mathcal{X’}$的时候Mixup的对象给包含了无标注数据, 因此在Mixup时需要让$\mathcal{X’}$的标签占据主导. 实际实现过程中, 我们取$\alpha=0.75$, 这是一种概率质量集中于两头的Beta分布. 同时在$\hat{X}$前的权重一般取生成的$\lambda \sim Beta(\alpha,\alpha)$ 中 $\max (\lambda,1-\lambda)$ 的值.
Virtual Adversarial Training(VAT)
对训练数据进行扭曲/加入噪声/Dropout都是针对于输入空间/中间特征空间的先验增广, 而这些增广对于深度学习特征而言未必是可靠的. 基于深度学习可以被对抗攻击这一特点, 一个很自然的想法是, 我们人为构造令标签变化最大的扰动, 然后对该扰动构造标签的正则化项作为差异学习目标。文献[8]首先提出了该算法, 一个简单的生成正则化损失函数的算法如下
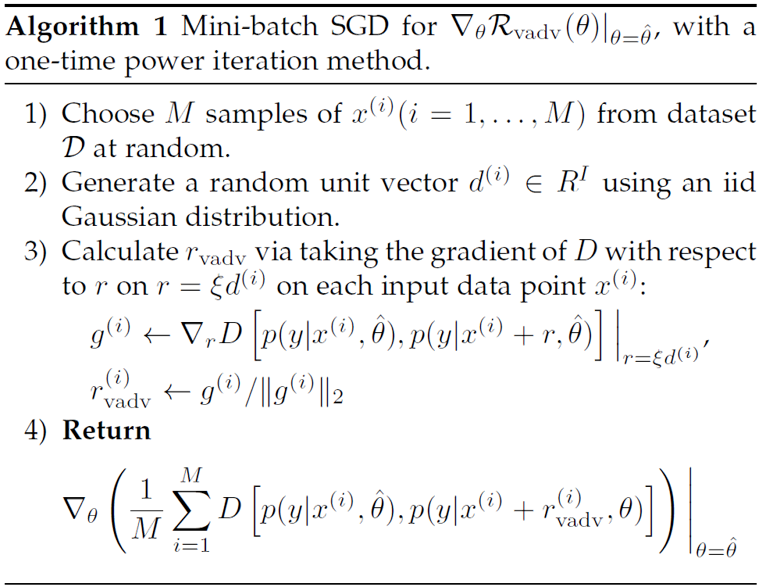
结合分类损失便构成了整个半监督学习算法。该方法在Cifar10上达到了13.13%的误差, 在SVHN上达到了5.63%的误差.
Mean-Teacher Method
Mean-Teacher[10]方法其实是受$\Pi$-model所启发, 但是它把滑动平均法扩展到了整个模型, 因此我们单独拿出来讨论。Mean Teacher方法复制了两个相同的网络(不同初始化), 一个称为Student网络, 另外一个称为Teacher网络。在训练过程中, Student网络通过学习损失来更新参数, 而Teacher网络利用Student网络更新过的参数与上一轮Teacher网络的参数进行滑动平均来更新参数. 第k个epoch中, 正则化损失的target$\tilde{z}_i$由Teacher网络生成, 在前向计算的过程中, 模型在两个网络的输入层和中间特征层均加入噪声, 详细算法图解如下
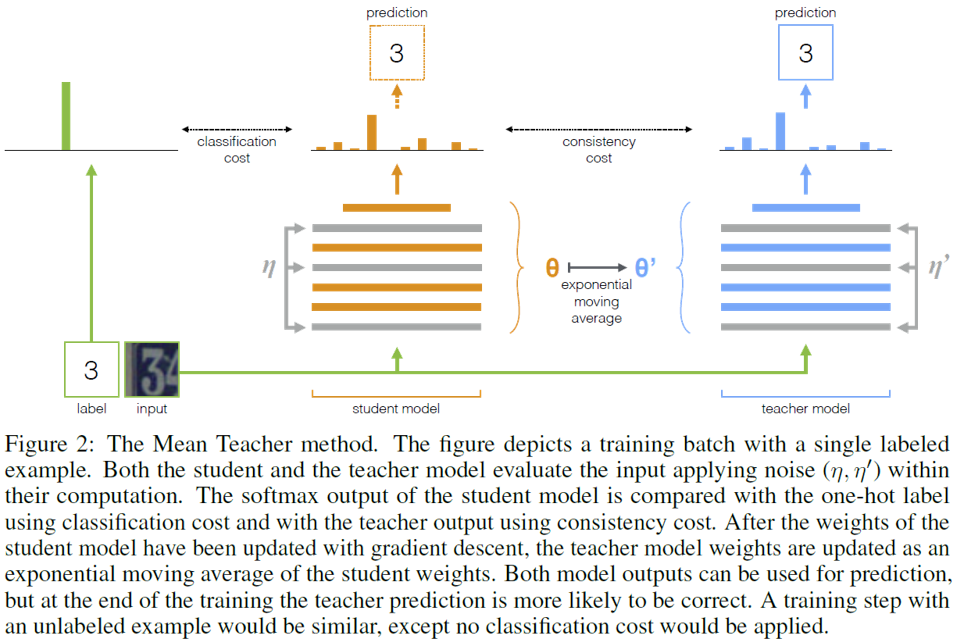
作者指出, 最终Teacher网络可以学到更好的半监督效果, 该方法分别达到了Cifar10 15.87%, SVHN 5.65%的错误率(讲道理这种方法能work确实是见了鬼了, 玄学吧woc…).
Entropy Minimization
文献[11]提出了基于最小化熵的差异正则化损失, 目的是让模型的预测所包含的不确定度更小, 这也是一个非常自然的想法, 它构造的正则化损失函数为:
\[L_u = \sum_{x_i\in \mathcal{D}_u}H(f(x_i))\]这个当然现在一般是当半监督学习的损失挂件在用, 有些算法加上这一项以后效果变好了, 比如VAT模型加了这一项以后在Cifar10上提升了7个千分点.
Pseudo-Labeling[12]
顾名思义, Pseudo-Labeling就是一个可以提供伪标签的算法. 简而言之, 就是对于无标签数据, 根据模型已经生成的预测选一些置信度比较高的预测并将这些预测one-hot化为伪标签训练无标注数据. 该方法真的非常直接, 不过训练trick比较多, 同时也引入了Entropy Minimization作为正则化项. 该方法的错误率为Cifar10 17.78%,SVHN 7.62%.
基于图模型的半监督学习算法
在现在的深度学习算法研究中,基于图模型的半监督学习并不是一个热门的方向,但是仍然有一些研究。一般而言,深度学习算法通过构造无监督任务,让网络学习一个样本间的相似度度量,然后对生成的拉普拉斯图矩阵添加标注,再用一些分类算法(kNN等)得到分类结果。构造实例区分(instance discrimination)任务是得到关系图的常用任务,如文献[14]就通过构造图像之间的实例分类任务得到相似度矩阵,然后通过kNN进行半监督分类。图模型的半监督算法结果并不出色,但是它的优势之处在于可以与主动学习等框架融合(如先学习一个度量,然后利用度量进行初步聚类,这样可以对聚类结果中的重要数据打上标签,提高打标签的效率).
Reference
[2] Goodfellow I, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets[C]//Advances in neural information processing systems. 2014: 2672-2680.
[3] Kingma D P, Welling M. Auto-encoding variational bayes[J]. arXiv preprint arXiv:1312.6114, 2013.
[4] Salimans T, Karpathy A, Chen X, et al. Pixelcnn++: Improving the pixelcnn with discretized logistic mixture likelihood and other modifications[J]. arXiv preprint arXiv:1701.05517, 2017.
[5] Xie Q, Dai Z, Hovy E, et al. Unsupervised data augmentation[J]. arXiv preprint arXiv:1904.12848, 2019.
[6] Berthelot D, Carlini N, Goodfellow I, et al. Mixmatch: A holistic approach to semi-supervised learning[J]. arXiv preprint arXiv:1905.02249, 2019.
[7] Dai Z, Yang Z, Yang F, et al. Good semi-supervised learning that requires a bad gan[C]//Advances in neural information processing systems. 2017: 6510-6520.
[8] Miyato T, Maeda S, Koyama M, et al. Virtual adversarial training: a regularization method for supervised and semi-supervised learning[J]. IEEE transactions on pattern analysis and machine intelligence, 2018, 41(8): 1979-1993.
[9] Laine S, Aila T. Temporal ensembling for semi-supervised learning[J]. arXiv preprint arXiv:1610.02242, 2016.
[10] Tarvainen A, Valpola H. Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results[C]//Advances in neural information processing systems. 2017: 1195-1204.
[11] Grandvalet Y, Bengio Y. Semi-supervised learning by entropy minimization[C]//Advances in neural information processing systems. 2005: 529-536.
[12] Lee D H. Pseudo-label: The simple and efficient semi-supervised learning method for deep neural networks[C]//Workshop on Challenges in Representation Learning, ICML. 2013, 3: 2.
[13] Diederik P. Kingma, Shakir Mohamed, Danilo Jimenez Rezende, and Max Welling. Semisupervised learning with deep generative models. In Advances in Neural Information Processing Systems 27: Annual Conference on Neural Information Processing Systems 2014, December 8-13 2014, Montreal, Quebec, Canada, pp. 3581–3589, 2014.
[14] Wu Z, Xiong Y, Yu S X, et al. Unsupervised feature learning via non-parametric instance discrimination[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018: 3733-3742.