参考资料:
FengHZ’s Blog 首发原创
笔记大纲
我们在之前的笔记中已经讲过了用KL散度进行两个分布的相似度度量, 但是, KL散度具有非对异性，值域无限，同时因为其具有$\log(\sigma_{i,i})$这一项，用于深度学习的反向传播过程中容易出现梯度爆炸等情况，这导致了用KL散度进行分布的距离度量在深度学习训练中的不稳定性。针对这三种问题，前人基于KL散度的基本形式用f-divergency给出了一些修正, 包括
-
Total Variation
\[dist_{tv}(F,G)=sup_{A}\vert F(A)-G(A)\vert = \frac{1}{2}\int_{\Omega} \vert p-q\vert dv\]其中第二个等号的证明如下，主要利用的结论为
\[B=\{x\in \Omega:p(x)>q(x) \},\int_{\Omega}\vert p-q \vert dv=\int_{B}\vert p-q \vert dv+\int_{\Omega- B}\vert p-q \vert dv;\\ \int_{B} p-q \ dv = \int_{\Omega- B} q-p \ dv\] - \[dist_{H}(F,G)=\sqrt{\frac{1}{2}\int _{\Omega}(\sqrt{p}-\sqrt{q})^2 dv}\]
本文将简要介绍基于最优传输理论所导出的Wasserstein距离，它有对称性，对于正态分布存在比较简单的闭式解，同时计算过程中没有$\log$函数的困扰，比较适合深度学习使用。同时, Wasserstein距离有着最优传输这一简洁直观的解释, 在很多分布度量性方面有着比$f-divergency$更优越的结果。
本文将首先介绍最优运输问题(Optimal Transport)的定义与基本形式，然后自然地将其与Wasserstein距离建立联系，最后本文将简单以CMU的文献为基础介绍Wasserstein距离显著优越的几个情形，离散采样中Wasserstein距离的计算与在某些分布上的闭式解。
最优运输问题的定义与基本形式
给定一个完备可分度量空间(Polish空间)(见附录)$X$, 我们用$\mathcal{P}(X)$来表示在$X$上的Borel概率测度的集合(也就是说$\forall u\in \mathcal{P}(X)$,$u$是一个概率测度,注意我们可以把$u$看成是一个分布函数，而不是概率密度,$du(x)=p(x)dx$才是概率密度).
如果$X,Y$是2个Polish空间, $T:X\rightarrow Y$是一个Borel映射(见附录), 同时$u\in \mathcal{P}(X)$, 我们诱导
\[u\rightarrow T_{\#}u\in \mathcal{P}(Y)\]满足
\[\forall E\subset Y, T_{\#}u(E)=u(T^{-1}(E))\]假定对于$X\times Y$空间, 我们定义了一个费用函数用以度量将$x\in X$转移到$y \in Y$的损失
\[c:X\times Y \rightarrow R^{+}\cup{+\infty}\]同时, 每一个$x$所占据的质量为$du(x)$,每一个$y$所占据的质量为$dv(y)$, 那么对于满足
\[T_{\#}u=v,T\in \mathcal{T}\]的最优运输策略$T:X\rightarrow Y$而言, 它的损失为:
\[\int_{x\in X}c(x,T(x))du(x)\]因此我们可以构造$\mathcal{T}\rightarrow R$的映射
\[T\rightarrow \int_{x\in X}c(x,T(x))du(x)\tag{1}\]而寻找$T$使得$(1)$取得最小值的过程可以用变分法求解，我们将
\[\inf_{T}\int_{x\in X}c(x,T(x))du(x)\tag{2}\]称作Monge视角下的最优运输问题.注意到在这个问题中，$x$是不可分的，也就是说只能把一个$x$移动到一个$y$位置，而不能将一个$x$进行细分并移动到多个$y$位置, 这就导致了令$(1)$式取最小值可能没有解，甚至$\mathcal{T}$空间可能是$\emptyset$, 一个例子如下:
$u,v$为dirac-delta度量,令$u=\delta_0,v=\frac{\delta_{-1}+\delta_{1}}{2}$，假设
\[\exists T,s.t. T_{\#}u=v\]那么$v(1)=u(T^{-1}(1))=\frac{1}{2}$, 这与$u(x)$要么取0要么取1矛盾.
基于这个问题, 一个很自然的想法是让$du(x)$变得可分,也就是说此时$du(x)$可以分成很多份，同时用于接收的$v$也满足$dv(x)$可以分为很多份，这样$x$就可以细分并运送给不同的$y$位置了, 在这个视角下我们对最优运输问题有了新的定义,即Wasserstein形式的最优运输问题:
\[\inf_{\gamma}\int_{X\times Y}c(x,y)d\gamma(x,y)\tag{3}\]其中,$\gamma \in \mathcal{P}(X\times Y)$(可以理解为是$X,Y$的联合分布函数),满足
\[\gamma(A\times Y)=u(A),\forall A\in \mathcal{B}(X);\gamma(X\times B)=v(B),\forall B\in \mathcal{B}(Y)\]它的一个等价形式是:
\[\pi^{X}((x,y))=x,\pi^{Y}((x,y))=y,\forall (x,y)\in X\times Y\\ \gamma\ s.t.\pi^{X}_{\#}\gamma =u;\pi^{Y}_{\#}\gamma =v\]其中$\gamma$则被称为是最优运输方案, 假定$\exists \gamma’$为 $(3)$ 式的最优解，那么我们可以理解$d\gamma’(x,y)$为将$du(x)$质量的位于$x$位置的物品切片播撒到$Y$空间的每一个位置，其中任意一个位置$y\in Y$的物品质量为$d\gamma(x,y)$,它们满足
\[\int_{y}d\gamma(x,y)=du(x),\int_{x}d\gamma(x,y)=dv(y)\]从最优运输问题到Wasserstein距离
从$(3)$式中我们可以很自然地推广到两个分布$X\sim P,Y\sim Q$之间的Wasserstein距离. 一个很自然的想法是，因为$X,Y$都是$R^d$空间，因此可以令$c(x,y)=\Vert x-y\Vert^p$,同时已知$P(x),Q(y)$的情况下我们可以有:
\[W_p(P,Q)=(inf_{\gamma\in \Gamma(P,Q)}\int_{x}\int_{y} \Vert x-y\Vert^pd\gamma(x,y))^{\frac{1}{p}}\tag{4}\]我们可以通过变分方法证明, 令$(4)$有解的$\gamma$是存在的，同时$(4)$存在对偶形式,即
\[W_p(P,Q)^p=sup_{\phi,\psi}\ \int \psi(y)dQ(y)-\int \phi(x)dP(x)\tag{5}\\ \psi,\phi :R^d\rightarrow R,s.t.\vert \psi(y)-\phi(x)\vert\leq \Vert x-y\Vert^p\]当$p=1$时, $(5)$可以简单化为:
\[W_1(P,Q)=sup_{\phi}\ \int \phi(y)dQ(y)-\int \phi(x)dP(x)\\ s.t. \phi:R^d\rightarrow R,\vert f(x)-f(y)\vert\leq \Vert x-y \Vert\]当$d=1$时(此时对$p$没有要求)，对于一元函数问题，我们可以给出简单的闭式解:
\[W_{p}(P,Q)=(\int_{0}^{1}\vert F^{-1}(z)-G^{-1}(z)\vert ^p)^{\frac{1}{p}},F,G\text{ are the cdf's of }P,Q\tag{6}\]Wasserstein距离的优越性,计算方法与闭式解
Wasserstein距离的优越性
有6个例子可以说明Wasserstein距离的优越性:
- f-distance无法很好地度量离散分布与连续分布的相似度, 假设$P$为$[0,1]$区间上的均匀分布, $Q_N$是均匀取值为${0,1/N,2/N,…,1}$的离散分布. 一个显然的事实是$Q_N\rightarrow P,N\rightarrow \infty$,因此$dist(P,Q_N)$应该为$N$的减函数。但是用Total Variation进行度量时,其结果始终为1(Trival), 而Wasserstein距离的结果为$\frac{1}{N}$, 这就更加有说服力了(按(6)式进行简单计算即可)
- f-distance丢失了空间中的几何特征.
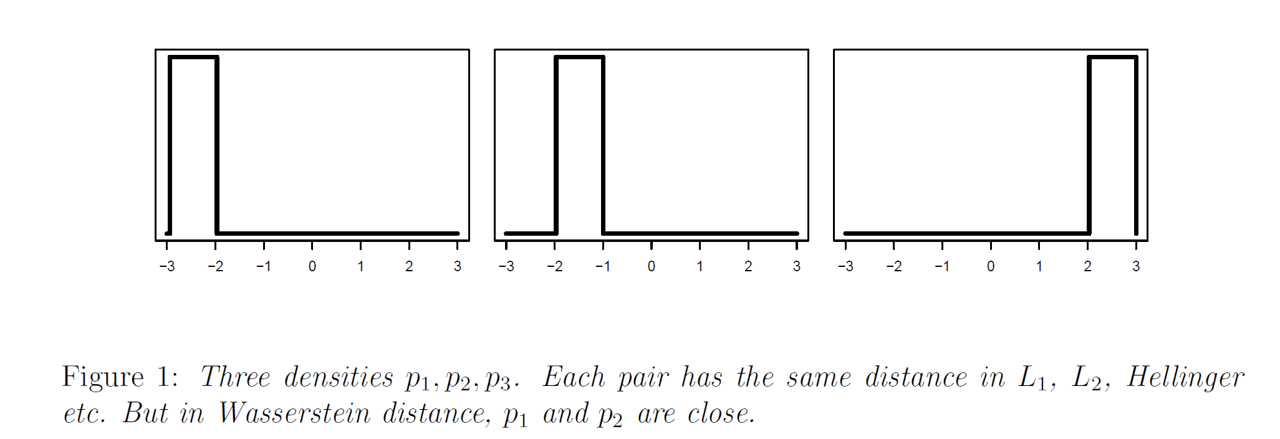如图所示为3个分布, 在f-distance下这三个分布两两距离相同, 但是在wasserstein-distance下$W(p_1,p_2)<W(p_1,p_3)$, 这个更加符合直观. - 用wasserstein-distance可以诱导出更自然的概率平均.
图中顶部的每一个正方形中的圆圈代表一种分布在圆周上的均匀分布, 底部左边是按$P=\sum_{i=1}^n P_i$进行概率平均所得到的分布函数结果，而底部右边则是按
\(P=argmin \sum_{i=1}^n W(P,P_i) \tag{7}\)
所得到的Wasserstein平均分布.我们可以很自然地看出用$(7)$所得到的平均分布更能刻画分布的特征. - 我们用f-distance进行分布距离计算时, 得到的度量只是一个序关系, 它并没有解释分布到底在哪里不同.但是当我们计算Wasserstein距离时, 我们得到了一个最优运输方案, 它告诉我们一个分布是如何变成另外一个分布的, 具有更强的可解释性.
-
如果我们要得到在两个分布$P_0,P_1$间的”插值”$P_t$,我们自然希望这个插值展现的是一个不改变分布基础形态特征(有几个峰,峰多高)的连续变化.
\[P_t=F_{t\#}\gamma'\]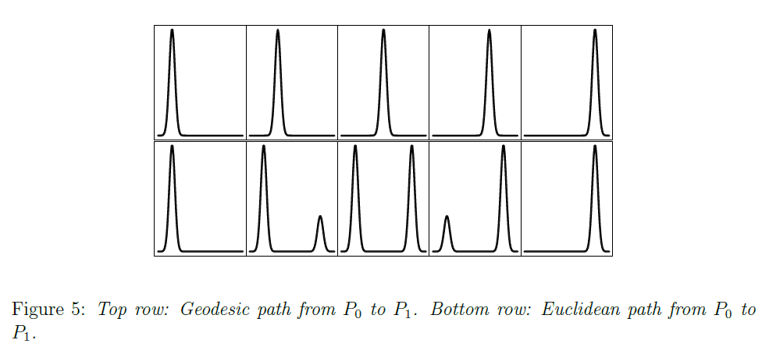
如图所示, 图底部展示了用$P_t=(1-t)P_0+tP_1$的变化，它破坏了分布函数的基础特征，而图顶部则用了的插值变化, 其中$\gamma’$是令$(4)$中$W(P_0,P_1)$取得最小值的”运输方案”,$F_t(x,y)=(1-t)x+t(y)$
- Wasserstein距离对于强烈的局部扰动并不敏感. 考虑$[0,1]$区间上的均匀分布$P$与定义在$[0,1]$区间上的密度函数为$1+sin(2\pi kx)$的分布$Q$而言,随着$k$的增大,函数$sin(2\pi kx)$的周期变小，频率变大，震荡更快, 但是其实随着$k\rightarrow +\infty$,$Q$应该更加接近于均匀分布, 此时$W(P,Q)=O(\frac{1}{k})$更加合理
Wasserstein距离的计算方法
$(6)$式给出了一元密度函数下的$W_p$距离简洁的计算方法，因此对于$d\geq 2$的情形, 我们可以将其与一元密度函数建立联系.假设此时有$R^d$空间中的分布$x\sim P,y\sim Q$, 我们取$R^d$空间球面上均匀分布的随机变量$\theta$,构造$P_{\theta}$为$x^{T}\theta$的密度函数, $Q_{\theta}$为$y^{T}\theta$的密度函数, 它们都是一元密度函数，我们定义sliced Wasserstein distance,S为
\[S(P,Q)=(\int W_p^p(P_{\theta},Q_{\theta})d\theta)^{\frac{1}{p}}\]同时，假设我们有一维密度函数$P,Q$分布的两组离散采样${X_1,\ldots,X_n},{Y_1,\ldots,Y_n}$, 我们可以采用次序统计量来计算$W_p(P,Q)$
\[W_p(P,Q)=(\sum_{i=1}^n\Vert X_{(i)}-Y_{(i)}\Vert^p)^{\frac{1}{p}}\]Wasserstein距离的闭式解
这里不加证明地给出几种分布的Wasserstein距离的闭式解:
-
Normal distributions
\[\mu_1=\mathcal{N}(m_1,C_1),\mu_2=\mathcal{N}(m_2,C_2)\\ W_2(\mu_1,\mu_2)^2=\Vert m_1-m_2 \Vert_2^2+ trace(C_1+C_2-2(C_2^{1/2}C_1C_2^{1/2})^{1/2})\]
附录(名词解释)
-
完备可分度量空间:一个完备度量空间是可分的当且仅当它存在一个可数稠密子集，或者说空间上存在一个序列
\[\{x_n\}_{n=1}^{\infty}\]满足该空间中的任意一个开子集都至少包含该序列中的一个元素. R是完备可分度量空间, $R^n$也是.
- Borel集:由R上所有左开右闭区间所组成的$\sigma$代数
- Borel映射:从拓扑空间$X\rightarrow Y$的Borel映射满足对于$Y$中任意开集, 闭集以及Borel子集, 它的原象都是$X$中的Borel子集.