FengHZ's Blog Summer is for falling in love.

Some useful tricks in training variational autoencoder

2018-11-27
机器学习

简介

训练变分自编码器(Variational AutoEncoder, VAE)并不是一件容易的事情，在VAE非常Fancy的模型背后，其训练过程非常不稳定。在本文中，笔者回顾自己在LIDC-IDRI以及MNIST数据集上的训练经验，给出一些训练的技巧，它们包括:

  1. VAE损失函数正则化参数的设置与主次矛盾分析
  2. 损失函数在pytorch中的写法与学习率设置
  3. 特征空间维数设置
  4. VAE结果可视化技巧

VAE训练经验与技巧总结

关于VAE的基本细节，可以参考我另外一篇Blog: An introduction to Variational Autoencoders

损失函数回顾

VAE的损失函数旨在最大化输入空间样本$(X_1,\ldots,X_n)$的出现概率，即最大化

\[\sum_{i=1}^{n}log(P(X_i))\tag{1}\]

由公式:

\[log(P(X))-\mathcal{D}[Q(z\vert X)\Vert P(z\vert X)]=E_{z\sim Q}[log(P(X\vert z))]-\mathcal{D}[Q(z\vert X)\Vert P(z)]\tag{2}\]

我们将最大化$(1)$转变为最大化$(2)$式右边项，构成了VAE的损失函数。我们对$X$关于$z$的后验，$z$关于$X$的后验与$z$的先验使用正态假设，即假设

\[P(X\vert z;\theta) \sim\mathcal{N}(X\vert f(z;\theta),\sigma^2*I) \tag{3}\] \[Q(z\vert X)\sim N(z \vert \mu(X;\theta),\Sigma(X;\theta)) \tag{4}\] \[P(z)\sim N(0,I)\tag{5}\]

同时，我们采用重参数化技巧计算$E_{z\sim Q}[log(P(X\vert z))]$，得到

\[E_{z\sim Q}[log(P(X\vert z))] \approx -\frac{1}{2}\frac{\Vert X-f(z;\theta) \Vert^2}{\sigma ^2}\tag{6}\]

采用正态分布的$KL$散度计算公式有

\[\mathcal{D}[Q(z\vert X)\Vert P(z)]=\frac{1}{2}[\Vert \mu(X;\theta) \Vert_2^2+\sum_{i}\Sigma(X;\theta)_{i,i}^2-\sum_{i}ln(\Sigma(X;\theta)^2_{i,i})-1]\tag{7}\]

因此$(2)$式最终可以写为：

\[\frac{1}{2}(-\frac{\Vert X-f(z;\theta) \Vert^2}{\sigma ^2}+[\Vert \mu(X;\theta) \Vert_2^2+\sum_{i}\Sigma(X;\theta)_{i,i}^2-\sum_{i}ln(\Sigma(X;\theta)^2_{i,i})-1]\tag{8}\]

去掉常系数$1/2$与常数项，将最大化写成最小化形式有

\[\frac{\Vert X-f(z;\theta) \Vert^2}{\sigma ^2}(part.1)-[\Vert \mu(X;\theta) \Vert_2^2+\sum_{i}\Sigma(X;\theta)_{i,i}^2-\sum_{i}ln(\Sigma(X;\theta)^2_{i,i})-1] (part.2)\tag{9}\]

该损失函数由两部分组成，第一部分$(part.1)$是基于二次重构误差的损失，需要手动设置超参数$\sigma^2$.第二部分$(part.2)$是基于$N(0,I)$的正态性先验假设下对于潜变量空间$P(z\vert X)$分布的约束，它的目的是让整个函数不因为仅优化重构误差而使得潜变量空间的分布距离太远。

从直观上来看，$(part.1)$使得从潜变量近似分布$Q(z\vert X)$中采样$z$所重构的$P(X\vert z)$概率最大，而$(part.2)$可以视作一个正则化项，它以$N(0,I)$作为正则化目标(此处可以比对参数正则化，参数正则化是以0为目标的)，目的是使得模型不完全过拟合重构误差，并在潜变量空间上对重构过程进行限制(即让模型更多关注于生成空间本身，而不是重构得更好)。

技巧与经验分析

训练失败的可能情况

在VAE训练的过程中，一个很典型的失败情况是$(9)$式不断下降，但是重构出来的图像是没有意义的噪声，在LIDC-IDRI数据集与MNIST数据集上的两个重构失败的典型图像如下所述:

vae_failed

在此图中，右上角为原始图像，其他为VAE的重构图像。注意到重构图像并不是一堆杂乱无章的噪声，而是彼此非常相似的，有某种分布的噪声，比如$(a)$图重构图像呈现两边白，中间黑的趋势，而$(b)$图则是呈现出中间杂乱的白色与两边统一的黑色。这是因为在这种情况下，$(9)$式中的$(part.2)$部分的$KL$损失会变成0，这也就意味着无论什么样的输入图像，模型都会将其映射到分布为$N(0,I)$的潜变量空间，在这种限制下，为了让$\frac{\Vert X-f(z;\theta) \Vert^2}{\sigma ^2}$这一部分最小，也就是最小化Mean-Square-Error，此时会让$f(z;\theta)\rightarrow \frac{1}{N}\sum_{i=1}^NX_i$，也就是说，此时重构误差会向输入的所有采样的均值回归，这就导致了以上两种情况的发生，即网络对于任意输入都映射到$N(0,I)$的分布，再将任意$N(0,I)$的采样潜变量映射到所有输入的均值。此时网络陷入局部极小值($KL$散度带来的梯度为0，同时均值回归使得$part.1$部分梯度也为0)，同时没有动力让其跳出局部极小值，因此导致了该现象发生。

LIDC-IDRI 与 MNIST数据集训练过程简述

对于LIDC-IDRI数据集，本文对其肺结节形态构建了变分自编码器，网络结构如图所示：

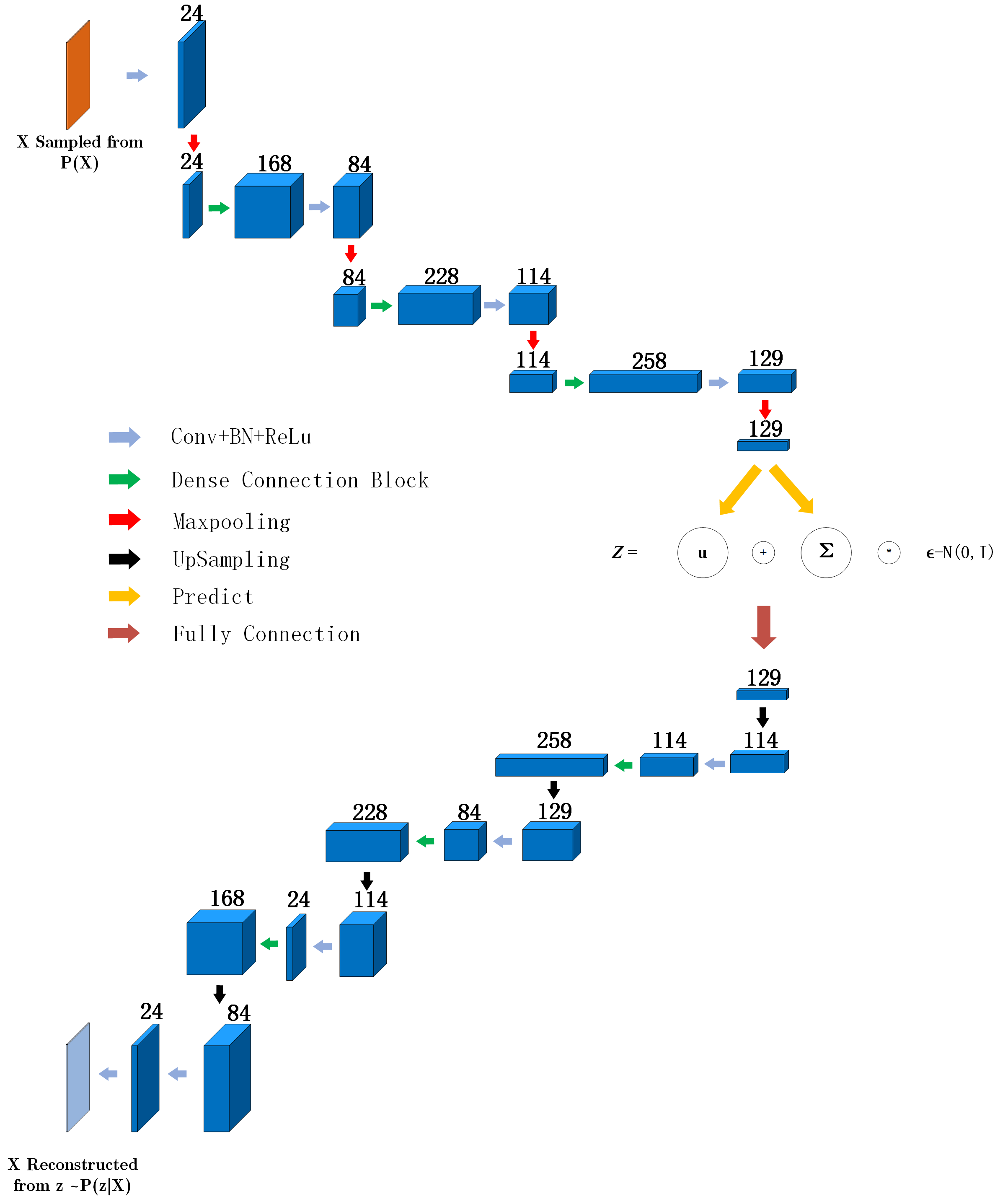
network_structure

对于MNIST数据集，我们采用Github-VAE中采用的由两个全连接层构成的VAE网络。

解决重构噪声问题

从上文中重构噪声的产生原因来看，解决重构噪声的问题的关键是增大重构误差(即$part.1$部分)的权重。如何增加这一部分的权重有两种方法。

  1. 调整$\sigma^2$项

    $\sigma$默认设置为$1$，调整$\sigma^2$项是一个非常显然的想法。将$\sigma^2$视作是正则化参数$\lambda$，减小$\sigma$等价于增大重构误差的权重。

  2. 用sum代替mean

    我采用pytorch进行编程，而进行损失函数计算时一般会将式$(9)$写成这种形式：

    reconstruct_loss = F.mse_loss(x_reconstructed, x)/sigma**2
kl_loss = torch.mean(z_mean_sq + z_sigma_sq - z_log_sigma_sq - 1)

    这时我们相当于计算了$part.1$部分的均值以及$part.2$部分的均值，但是注意到$(9)$式中$part.1$部分以及$part.2$部分都是以sum形式呈现的，因此我们可以用用sum代替mean，同时注意到batchsize，还要对每个batchsize进行平均

    reconstruct_loss = F.mse_loss(x_reconstructed, x,reduction="sum")/(sigma**2*batch_size)
kl_loss = torch.mean(z_mean_sq + z_sigma_sq - z_log_sigma_sq - 1)/batch_size

    一般由于$dim(X)\gg dim(z)$，因此进行求和后 $part.1$ 部分的损失将远远大于$part.2$部分，(e.g. 对于肺结节 $64\times 64\times 64$的输入，对应于潜变量空间$dim(z)=256$，大概在最终收敛的情况下$\frac{part.1}{part.2}=5$)

训练中出现Nan的情况

在训练过程中，一个很容易出现的情况是$(9)$式中$part.2$部分出现Nan的问题。注意到上文中我们提过$part.2$部分主要起到在潜变量空间进行正则化的作用，因此这一部分的收敛轨迹是比较扑朔迷离的。同时由于$log$函数数值稳定性较差，容易出现$gradient=\infty$的情况，从而导致Nan的问题出现。我们可以用三种方法对该问题进行解决。

  • 调整学习率

    将学习率尽量设低有助于避免Nan问题。如果我们按”用sum代替mean“的流程进行操作，那么一般推荐学习率为$1e-7,1e-8,1e-9$之间，此时可以缓和$\log$函数带来的梯度爆炸问题。

  • 预测log_sigma代替直接预测sigma

    注意在潜变量空间中，我们预测输入$X$对应的$Q(z\vert X)\sim N(z \vert \mu(X;\theta),\Sigma(X;\theta))$，也就是说，预测$\mu,\Sigma$。 一般因为$\Sigma$是一个对角矩阵，因此我们仅仅对对角元进行预测，即预测$\Sigma_{ii}=\sigma_i$，但是这就需要对$\sigma_i$进行$\log$计算。同时pytorch的log函数数值稳定性是真的差，因此我们可以预测$\log(\sigma_i)$来代替对$\sigma_i$进行直接预测。

  • 梯度clip

    还有一种比较粗暴的手段是直接对梯度进行clip操作，即将梯度控制在某个范围内。一般可以取$1e5$范围

    torch.nn.utils.clip_grad_value_(model.parameters(), 1e5)

    这样就可以避免梯度爆炸

如何判断训练过程是否正常

一般可以对$(9)$式的损失函数进行分$part$的绘制并查看损失函数结果。损失函数应该呈现如下形状：

  1. $part.1$部分的损失函数应该是呈现初期迅速下降，后期缓慢下降的态势
  2. $part.2$部分的损失函数是用$N(0,I)$对潜变量空间进行约束，在初始阶段应该呈现上升趋势，然后再在中途稳定下降，一开始的上升是为了保证重构误差下降，在重构误差下降中，自然会将输入$X$先大幅度偏离既定的潜变量空间，然后再在训练过程中慢慢拉回$N(0,I)$的空间中。

一个典型的例子为：

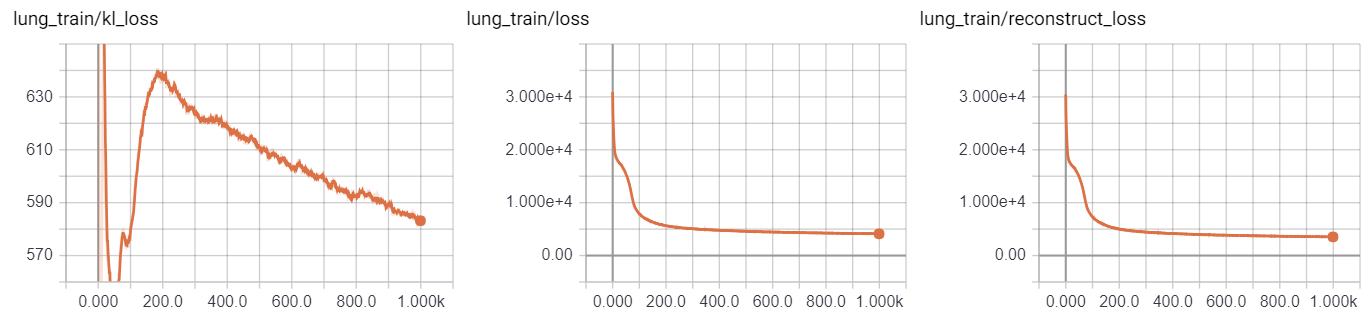
loss_curve

在这个例子中，kl_loss即$part.2$部分损失，它呈现先上升后下降的态势，而重构误差(reconstruct_loss)则呈现迅速下降，缓慢下降，更缓慢下降的三段态势。

潜变量空间维数设置

潜变量空间维数$dim(z)$是变分自编码器训练过程中最重要的超参数，对它的设置将影响到整个VAE的训练质量。

如果潜变量空间维数设的太大，就会导致潜变量空间的约束太少，不能正确拟合流形假设，同时潜变量空间维数过大会导致潜变量的数据分布过于稀疏(考虑高维正态分布其实会和均匀分布非常像这个直观)，甚至导致很多维数的语义是重合的，因此在用潜变量空间度量相似度的时候会因为维数过高出现偏差。

而如果潜变量空间维数设置太小，则会导致对流形的拟合是残缺的，是一个近似(类似于泰勒展开只展开了前3项吧)，同时在潜变量空间进行分类可能会出现错误(如大量语义信息未被编码等)，但是潜变量空间维数设置小一点的后果不会像维数太大一样严重。

因此两个比较简单的潜变量空间维数选取原则是:

  1. 选取的维数能够令重构图像尽量还原输入图像
  2. 尽量设置比较小的维数

一个采用$PCA$方法进行潜变量空间设置的迭代启发式算法可以如下所述：

  1. 设置较大的空间维数(如设置$dim(z)=1024$)
  2. 训练VAE直到收敛
  3. 对所有的输入图像潜变量空间的均值$\mu(X;\theta)$进行预测，然后采用主成分分析法对$\mu$进行降维处理，保证选取的维数$k$能够解释$90\%$以上的方差,并令$dim(z)=k$
  4. 迭代2,3，直到选出满意的$dim(z)$

VAE结果可视化方法

本节我将以Sampling Generative Networks一文为主要参考文献，简单介绍对图像生成模型结果进行评价与可视化的一些方法。我将以LIDC-IDRI数据集作为主要例子。

Code还没写好，太监一下。

上一篇 Some notes on variational inference

下一篇 Denoising Criterion for Variational Autoencoding Framework

Comments

Content