FengHZ‘s Blog首发原创
简介
从主成分分析(PCA),线性因子模型到自动编码器,基于无监督学习的特征提取方法不断发展。同时自从引入深度学习技术后,我们对潜变量与因子空间的推断效率与推断方法都有极大的突破,此时原始数据可以在因子空间(通常是潜变量空间)得到更简洁的表示。一个很自然的问题是,如何来比较两种表示的优越程度呢?到底是什么因素决定了一种表示比另外一种表示更好呢?
No Free Lunch Theorem告诉我们,所有的机器学习算法的期望效果都是一样的,但是有一些算法在特定的任务上表现会更好。因此,表示的优劣与否往往取决于我们采用该表示与所进行的学习任务是否契合。但是表示学习方法往往是无监督的,如何在无监督过程中注入我们将要进行的学习任务的偏好,以使得某一种表示方法在某种任务上优越于其他表示方法,这就是表示学习领域所关注的任务。
表示学习指出,我们可以以潜先验(meta-prior)的形式为模型注入关于潜变量的一些先验信息,如潜变量的独立性信息,层次信息,因果信息,稀疏性信息等,以使得模型能够令表示体现相应的特征。这些潜先验可以用模型约束的形式注入(如稀疏性信息可以用一阶正则化项表示),可以作用于模型结构上(如层次信息可以用feature pyramid表示),也可以用统计推断方法的后验概率独立性进行约束(如VAE的潜变量后验概率),同时,我们更可以用半监督学习方法(semi-supervised learning)来迫使模型习得我们所偏好任务的因果关系。表示学习认为,如果表示向量$\mathbf{h}$表示观察值$\mathbf{X}$的很多潜在因素,而我们的任务所需要推断的因素$\mathbf{y}$恰好包含在$\mathbf{h}$中,那么通过$\mathbf{h}$来预测$\mathbf{y}$将非常容易。
表示学习与深度学习的结合力量是非常强大的,深度学习是一般函数近似任务的几个世纪进步的结晶,它作为万能近似工具可以轻松地学习到任何变量间的映射关系,而表示学习则为深度学习提供了正确的学习方向。
本文旨在对表示学习领域进行初学者的阶段性总结式介绍,并梳理从表示学习到变分自动编码器之间的关系。本文主要参考资料为Deep Learning Book中的13,14,15,19章。本文将以抽象层次由低到高的顺序展开,在Section.1中,本文将介绍PCA与线性因子模型的主要假设与结构, 在Section.2中,我们将PCA扩展到非线性PCA,同时引入自动编码器这个概念,并给出自动编码器的一些约束模式,在Section.3中,我们将这些约束模式放在表示学习(representation learning)的框架下进行讨论,并引入无监督预训练(unsupervised pre-training),迁移学习与领域自适应(transfer learning and domain adaptation),半监督学习(semi-supervised learning),特征分布式表示(distributed representation)以及潜先验(meta-prior)这些表示学习的热门领域,从而对表示学习进行概览。最后,我们将研究表示学习领域下的一类强力的非线性因子模型变分自动编码器(VAE),在此前的BlogAn introduction to Variational Autoencoders,以及Some notes on hierarchical vae中,我们已经对(VAE)有了一个比较全面的了解,本文主要将重点放在变分推断的发展历程与假设分析方面。
Section.1 线性因子模型
PCA与因子模型
PCA与因子模型是两大主要的降维模型,虽然在求解技术方面,两大模型在正态假设下都对协方差矩阵施加特征值分解变换以在有限维度下求得包含最大方差的变换,但是在模型原理与模型解释方面两大模型有较大的差距。其中,PCA可以看作是自动编码器的一种简单情况,而因子模型则可以看作变分自动编码器的雏形,同时PCA可以施加概率变换变成因子模型。
模型结构
假设$\mathbf{X}=(X_1,\ldots,X_p)’$为$p$维随机向量,其均值为$E(\mathbf{X})=\mathbf{\mu}$,协方差矩阵$D(\mathbf{X})=\mathbf{\Sigma}$,PCA模型要求找到$\mathbf{h}=(h_1,\ldots,h_q)’$为$\mathbf{X}$的前$q$个主成分,满足
\[\begin{aligned} h_i &= \mathbf{a_i'}\mathbf{X}\\ \mathbf{a_i'a_i }&= 1, i = 1,\ldots,p\\ 当i>1,\mathbf{a_i'\Sigma a_j}&=0,j=1,\ldots,i-1\\ Var(h_i) &= \max_{a'a=1,a'\Sigma a_j=0,j=1,\ldots,i-1}Var(\mathbf{a'X}) \end{aligned}\]求解过程就是很简单的对对称半正定协方差矩阵$\mathbf{\Sigma}$进行正交分解
\[\mathbf{\Sigma} (\mathbf{a_1,a_2,\ldots,a_n})=\mathbf{\Lambda (a_1,a_2,\ldots,a_n)}\tag{1}\]然后对$\mathbf{\Lambda}=diag(\lambda_1,…,\lambda_p)$进行排序,满足$\lambda_1\geq \lambda_2\geq\lambda_p$,然后挑选出前$q$个$\mathbf{a}$,得到$\mathbf{h}$,此时$Var(h_i)=\lambda_i$,同时$h_i,h_j$线性无关。
注意到PCA所分解的对象$\mathbf{X}$仍然是随机变量,但是PCA所用的手法却属于数值代数的范畴。PCA等价于一个坐标旋转变换,它将数据协方差矩阵进行了旋转,并在新的坐标系上进行了投影,然后只选择那些投影度量比较高的分量作为最后的结果,它的几何解释可以参考下图。
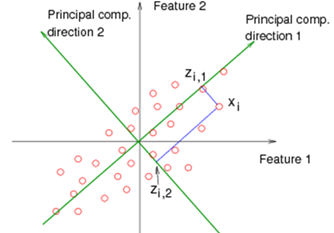
因子模型可以看作是一个生成模型,它描述了一个以潜变量$\mathbf{h}$为因,以可观测变量$\mathbf{X}$为果的生成关系。假定$\mathbf{h}\sim p(\mathbf{h})$, 其中$\mathbf{h}$满足独立性假设,即$p(\mathbf{h})$$=\Pi_{i=1}^{n}p(z_i)$。我们对$\mathbf{h}$进行一次观测,得到一个观测结果$\mathbf{\tilde{h}}$,然后用如下生成模式生成其对应的观测变量$\mathbf{\tilde{X}}$:
\[\mathbf{\tilde{X}} = \mathbf{W\tilde{h}+b+z},z\sim \mathcal{N}(\mathbf{0,\Phi *I}),\mathbf{\Phi}= diag(\sigma_1^2,\ldots,\sigma_p^2)\tag{2}\]它诱导出了$\mathbf{X}$关于给定$\mathbf{h}$后的后验概率$p(\mathbf{X}\vert \mathbf{h})$,其中$\mathbf{W}$是可求解的参数。一般我们拥有大量可观测变量$\mathbf{\tilde{X}}$,给定因子模型后,我们需要求得最优的$\mathbf{W,b}$。注意仍然可以用主成分估计来求解$\mathbf{W,b}$,注意到当$\mathbf{\Phi} \rightarrow 0$时,因子模型可以看成是PCA模型。
因子模型中的meta-prior
如果我们将已知大量可观测变量$\mathbf{\tilde{X}}$后的因子模型 $(2)$ 看作是一个统计推断问题, 即已知模型 $(2)$,给定一个新的样本 $\mathbf{X_{test}}$ 后,我们来推断到底是什么样的 $\mathbf{h_{test}}$ 生成了 $\mathbf{X_{test}}$,一个很自然的想法是最大似然估计,即找到单个最可能的编码值
\[\mathbf{h}^{*}_{test} = \arg\max_{\mathbf{h}} p(\mathbf{h}\vert \mathbf{x}) \tag{3}\]考虑贝叶斯公式:
\[p(\mathbf{h}\vert \mathbf{x}) = \frac{p(\mathbf{x}\vert \mathbf{h})p(\mathbf{h})}{p(\mathbf{x})}\]我们可以把$(3)$改写为:
\[\mathbf{h}^{*}_{test} = \arg\max_{\mathbf{h}} \log(p(\mathbf{x}\vert \mathbf{h})) + \log(p(\mathbf{h}))\tag{4}\]$(4)$将$\mathbf{h}$的先验与因子模型中$\mathbf{X}$的后验结合起来了,此时我们可以通过对$\mathbf{h}$的先验施加一些约束来体现meta prior,一个典型的例子是稀疏编码约束,即我们希望$\mathbf{h}$中是稀疏的,仅仅在几个分量上具有权重,这样可以将样本依据在各因子上的权重进行分类或聚类。
稀疏编码约束
一个典型的稀疏编码约束是将$\mathbf{h}$的先验看成Laplacian分布,即
\[p(h_i)=\frac{\lambda}{4}e^{-\frac{1}{2}\lambda \vert h_i \vert}\]此时$(4)$在因子模型与Laplacian分布下的解析形式为
\[\arg\min_{\mathbf{h}} \lambda \Vert \mathbf{h} \Vert_1+ \mathbf{(x-Wh)'\Phi^{-1}(x-Wh)}\]该形式对因子$\mathbf{h}$增加了一阶范数正则化,体现了稀疏编码约束。
不变特征(慢特征)分析
如果我们将$(4)$中计算$\mathbf{h}$的过程看作是一个关于$\mathbf{X}$的函数$\mathbf{h=f(X)}$,从这个视角下我们可以得到更多关于meta prior的形式,其中一个与时间序列数据有关的形式是不变特征(慢特征)分析。
慢特征分析是针对时间序列数据学习时序变化下不变特征的因子模型,它的想法来源于慢性准则(slowness principle),即虽然对于单一场景而言有很多变化迅速的变量,但是对于整个时序场景而言,构成整个时序场景主要语义的特征变化是缓慢的。比如说,对于计算机视觉而言,视频上的像素改变是非常快的,如一匹斑马泵跑的视频,每一个像素点将在黑白之间不断变换,可是表达”图中是否有一匹斑马”的特征在整个视频中并不会变化,同时表达”图中斑马的位置”的特征在整个视频中变化的也很慢。如果我们希望将”习得变化缓慢的特征”作为因子模型的meta prior的话,我们需要在损失函数中加入慢性正则化
\[\eta \sum_{t}L(f(x^{(t+1)}),f(x^{(t)})) \tag{5}\]SFA算法将函数$\mathbf{f(X;\theta)}$看作是优化参数$\theta$的问题(这个视角对于深度学习而言是非常自然的),并将慢性正则化条件改为求解优化问题
\[\begin{aligned} \min_{\theta} & E_{t}\Vert \mathbf{f(x^{(t+1)})-f(x^{(t)})} \Vert_2,\\ s.t. & \\ E_t \mathbf{f(x^{(t)})}_i&=0\\ E_t [\mathbf{f(x^{(t)})}_i]^2&=1 \\ E_t[\mathbf{f(x^{(t)})}_i\mathbf{f(x^{(t)})}_j]&=0,\forall i < j \end{aligned}\]这些慢性条件可能可以在序列预测中得到一些好的结果,如果我们对物体运动环境已经进行了详细了解(如3D渲染环境的随机运动中,我们需要对相机位置,速度概率分布进行了解),那么SFA算法能够比较准确地对深度模型预测SFA将学到什么样的特征。但是,慢性条件仍然没有大规模进行使用,这可能是因为慢性先验过于强大,使得模型对特征的预测坍缩到一个常数上,而无法捕捉时间上的连续微小变化。在物体检测方面,SFA能够捕捉到物体的位置特征,但是会忽视那些高速运动的物体。
Section.2 自动编码器
从PCA到自动编码器
对于$\mathbf{X}=(X_1,\ldots,X_p)’$为$p$维随机向量,其均值为$E(\mathbf{X})=\mathbf{\mu}$,协方差矩阵$D(\mathbf{X})=\mathbf{\Sigma}$,一个简单的自动编码器可以表示为
\[\begin{aligned} \mathbf{h=W^T(X-\mu)}\\ \mathbf{\hat{X} = g(h) = b+Vh} \end{aligned}\]我们希望它能够最小化重构误差
\[E[\Vert\mathbf{ X-\hat{X} }\Vert^2] \tag{6}\]我们可以证明,能使得$(6)$最小的解为$V=W,b=\mu$,其中$W$为$(1)$中PCA所对应的解。因此一个简单的线性编码器的编码部分即为PCA所对应的映射,而解码部分则为PCA的逆映射。如果$\mathbf{dim(h)=dim(X)}$,则在最优解下$(6)$为0,否则解码部分将会产生为$\sum_{i=\mathbf{dim(h)}}^{\mathbf{dim(X)}}\lambda_i$ 的损失。在这个例子中我们可以看到,PCA可以视作自动编码器的一种特殊情况。
自动编码器中的meta prior
为叙述方便,我们记编码函数为$f$,解码函数为$g$
欠完备自编码器
欠完备自编码器即限制$\mathbf{dim(h)< dim(X)}$,学习过程可以简单描述为最小化损失函数
\[L(\mathbf{x},g(f(\mathbf{x})))\]其中$L$为一个损失函数,对$g(f(\mathbf{x}))$与$\mathbf{x}$的差异进行惩罚,常用的损失函数如均方误差函数。正如上文所言,如果$f,g$都为线性函数,那么我们将学习到与PCA相同的子空间。如果$g,f$都是非线性的,那么我们将PCA推广为非线性。
正则自编码器
去噪自编码器
如果我们对输入加入噪声,构造$\mathbf{X}\rightarrow \mathbf{\tilde{X}}$,以及损失函数$L(\mathbf{X},g(f(\mathbf{\tilde{X}})))$,我们就利用噪声构造了去噪自编码器。它能够迫使模型专注于$\mathbf{X}$本身,忽略采样噪声。
$\nabla_{\mathbf{X}}\mathbf{h}$梯度作为正则
如果我们希望编码结果对于$X$的微小扰动是鲁棒的,从而在潜变量空间上呈现簇状聚类结果,那么采用$\nabla_{\mathbf{X}}\mathbf{h}$作为正则是一个可行的方法,具体而言,我们在损失函数中增加$\lambda \Vert \nabla_{\mathbf{X}}\mathbf{h} \Vert_2^2$,以令潜变量具有聚类特征。
稀疏正则化
如果我们将确定的$f,g$扩展为对$p_{model}(\mathbf{x\vert h})$的推断,并将损失函数关联$\mathbf{x}$的最大似然
\[\log p_{model}(\mathbf{x}) = \log \sum_{h'}p_{model}(\mathbf{(h',x)}) \tag{7}\]同时利用$\mathbf{h=f(x)}$来选择高似然点的$h$估计$(7)$,那么$(7)$可以估计为
\[\begin{aligned} \log p_{model}(\mathbf{x}) = \log \sum_{h'}p_{model}(\mathbf{h',x}) \approx \log p_{model}(\mathbf{h,x}) =\\ \log p_{model}(\mathbf{h}) + \log p_{model}(\mathbf{x\vert h}) \end{aligned}\]与Section.1中的稀疏编码约束相似,将$\mathbf{h}$的先验看成Laplacian分布,即
\[p(h_i)=\frac{\lambda}{4}e^{-\frac{1}{2}\lambda \vert h_i \vert}\]我们就得到了稀疏正则化项$\lambda\sum_{i} \vert h_i \vert$.
Section.3 表示学习
从PCA到线性因子模型,再到自动编码器,我们已经见过了很多表示学习算法以及在算法上施加的meta prior约束。在本节中,我们将这些约束模式放在表示学习(representation learning)的框架下进行讨论,并引入无监督预训练(unsupervised pre-training),迁移学习与领域自适应(transfer learning and domain adaptation),半监督学习(semi-supervised learning),特征分布式表示(distributed representation)以及潜先验(meta-prior)这些表示学习的热门领域,从而对表示学习进行概览。
无监督预训练
2006年,Hinton提出深度神经网络可以采用贪心逐层无监督预训练的方式找到一个良好的初始值,从而得到良好的收敛结果。这种预训练方式有两个亮点。一是贪心,即每次固定其他所有层参数,仅对某一层进行训练,二是无监督,即采用某种单层无监督表示学习算法让网络学习特征。结果表面,该算法能够缓解网络的过拟合问题,使其在测试误差上获得重大提升。然而,这种预训练方法也遵循No Free Lunch定理,即该初始化结果对于某一些任务而言是有极大负面影响的,因此划定无监督预训练的使用范围极为重要。
一般而言,我们认为无监督预训练在网络初始的表示很差的时候能够优化表示,这一技术在NLP中常常使用。NLP对于词的表示往往是用one-hot编码进行表示的,这种表示方法使得任意两个不同的词之间距离都是一样的,同时可能存在两段自然语言的语义完全不一样,可是距离却很近,因此one-hot编码并不是一个良好的表达。在该任务上采用无监督预训练可以获得良好的初始表示,从而使得从好的表示学习相应的任务变得容易。同时,无监督预训练也可以作为一种半监督学习算法发挥作用。如我们可以先用大量无标注数据进行无监督预训练,然后再用少量标注样本进行监督训练,这种方法从直观上来看可以利用更多信息,因此是奏效的。
深度学习发展至今,在NLP领域之外,无监督预训练所发挥的作用越来越少,Dropout和Batch Normalization作为深度神经网络的新技术取得了比无监督预训练更好的效果。但是,无监督预训练作为表示学习的基本思想之一仍然在发挥作用。ImageNet预训练技术已经成为计算机视觉任务中神经网络训练的必备技术,它可以大大减少收敛所需要的时间,同时在小数据集上达到更好的泛化结果。
迁移学习与领域自适应
无监督预训练已经具备了迁移学习的雏形,即将一个情景下所习得的表示应用于另一种情景的预测任务中去。这种方法能够奏效的前提是两种不同情景所需要的表示是相似的,这使得模型可以同时受益于两种情形的训练数据。
在迁移学习中,两种情形的输入是相同的,但是模型所要执行的任务不一样,但是我们认为两个任务都可以依赖于相同的表示进行微调(如两个任务所输出的不同向量$\mathbf{y_1,y_2}$都是相同的表示向量$\mathbf{h}$的重要原因,此时通过$\mathbf{h}$对$\mathbf{y_1,y_2}$预测都会很容易)。迁移学习一般体现在共享底层的框架(如深度神经网络的backbone与预训练参数等),而对任务相关的部分进行微调,ImageNet预训练就是典型的迁移学习场景。
在领域自适应问题中,不同情形的输入分布并不相同(如文本输入与图像输入),但是模型所要执行的任务是一致的。如在文本,图像,声音等领域分别进行情感预测,预测目标都是一样的,而输入并不一样,这就要求模型将不同的输入分布都映射到相同的表示,并利用表示进行预测。领域自适应一般体现在共享从表示到预测的部分,而对底层表示则需要分别学习,将不同输入映射到通用特征。
迁移学习的两种极端形式是一次学习与零次学习,只有一个标注样本的迁移任务称为一次学习,没有标注样本的迁移任务被称为零次学习。一次学习的可行性在于模型将相似类别的图像聚集在相似的表示下,因此仅凭借一个标签就可以代表该种聚集的表示。而零次学习则要求学习器已经习得了能够表示该类任务的额外信息,如已知猫有四条腿和尖尖的耳朵,那么学习器可以在没有见过猫的情况下猜测图像中猫的存在。一个零次迁移学习的图示如下:
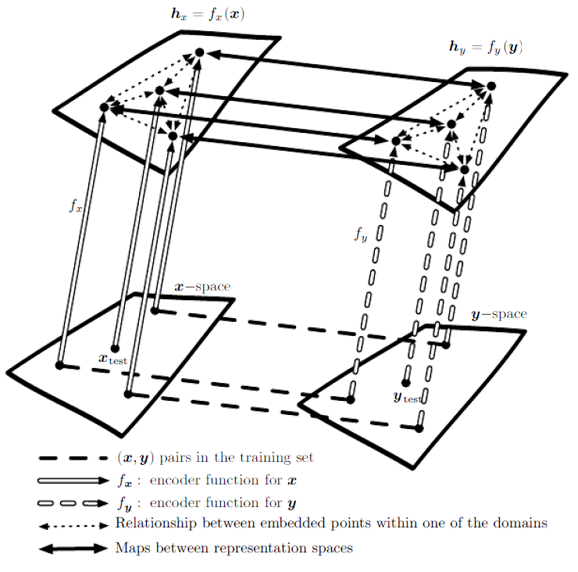
标注与未标注样本$\mathbf{x}$可以学习表示函数$f_{\mathbf{x}}$,同时,样本$\mathbf{y}$也可以学习表示函数$f_{\mathbf{y}}$。利用有标注的样本$(\mathbf{x},\mathbf{y})$我们可以学习从$f_{\mathbf{x}}(\mathbf{x})$到$f_{\mathbf{y}}(\mathbf{y})$的单项或双向映射,习得这种映射后,对从未出现过的对$(x_{test},y_{test})$我们也可以通过$f_{\mathbf{x}}(\mathbf{x_{test}}),f_{\mathbf{y}}(\mathbf{y_{test}})$彼此关联,从而实现零次学习。
半监督学习
我们已经讨论了很多无监督表示学习算法,并认为通过无监督所习得的表示向量$\mathbf{h}$表示观察值$\mathbf{X}$的很多潜在因素,而我们所要进行的某些特定预测任务的输出向量$\mathbf{y}$是最为重要的原因之一,那么用$\mathbf{h}$对$\mathbf{y}$进行预测将是高效且容易的。但是,无监督表示学习算法所习得的表示$\mathbf{h}$很有可能无助于学习$p(\mathbf{y\vert X})$,此时,我们就需要半监督学习来”迫使”模型习得某种适应于$\mathbf{(X,y)}$的关系,这就是半监督学习的意义所在,我们用生成模型来描述这种因果关系。
一般模型能够成功习得$p(\mathbf{y\vert X})$的前提在于$\mathbf{(X,y)}$并非是独立的,即它们本身具有因果关系,与因子模型一致,我们建立$\mathbf{(X,y)}$的生成关系。
假设$\mathbf{y}$是$\mathbf{X}$的成因之一,让$\mathbf{h}$代表所有这些成因。那么真实的生成过程可以认为是先从$\mathbf{h}\sim p(\mathbf{h})$对$\mathbf{h}$进行采样,同时依据采样$\mathbf{h}$生成$\mathbf{X\sim p(X\vert h)}$,即
\[\mathbf{p(h,X)=p(X\vert h)p(h)} \tag{8}\]在已知观测数据$\mathbf{X}$的前提下,我们可以利用$(8)$对$\mathbf{X}$施加极大似然约束
\[\max \mathbf{p(X)=\sum_{h}p(h,X)}\]从而对生成模型参数进行优化。一个理想的生成模型应该可以表示上述生成过程,其中$\mathbf{h}$作为潜变量解释$\mathbf{X}$中可观察的变化。如果$\mathbf{y}$与$\mathbf{h}$紧密关联,那么从$\mathbf{h}$对$\mathbf{p(y\vert X)}$进行推断是容易的。反之,如果我们已经有了$\mathbf{(X,y)}$,那么令网络半监督学习$\mathbf{h}$时也会迫使网络所习得的表示$\mathbf{h}$能够容易地对$\mathbf{p(y\vert X)}$进行推断。
在生成模型下进行半监督推断的另一个好处是能够刻画因果关系。生成模型中$\mathbf{X}$是结果,而$\mathbf{y}$则是原因,这种因果关系的好处在于模型$p(\mathbf{X\vert y})$对于$p(\mathbf{y})$的形式是鲁棒的(因为此时$\mathbf{p(y\vert X)=p(y)}$),从而可以忽视在数据集中$p(\mathbf{y})$先验发生强烈波动后的影响。如果因果关系逆转($\mathbf{p(X\vert y)=p(X)}$,则
\[p(\mathbf{X\vert y}) = \frac{\mathbf{p(y\vert X)p(X)}}{\mathbf{p(y)}}\]此时对于$\mathbf{p(X)}$的变化,$p(\mathbf{y\vert X})$变得鲁棒,而$p(\mathbf{X\vert y})$则对$p(y)$的变化十分敏感。
分布式表示
分布式表示是深度学习成功的关键之一,也是深度学习与表示学习紧密结合的理念。分布式表示的思想是,系统的每一个输入都应该由多个特征表示,并且每一个特征都应该参与到多个可能输入的表示中去。比如,假设我们有一个能够识别红色,绿色,或蓝色的汽车,卡车和鸟类视觉系统,表示这些输入的其中一个方法是将它们两两配对形成九个可能的组合,并使用单独的神经元或隐藏单元进行激活。如果我们有更多概念的话,需要表达它们的隐藏神经元数目是呈指数级增长的。改善这种情况的方法之一是分布式表示,即我们用三个神经元描述颜色,用三个神经元描述对象身份,并采用层次结构让输入在不同神经元上序贯激活,这使得模型隐藏神经元的数目是线性增长的。在计算机视觉任务中,由于输入物体往往是在语义层次具有区别,在特征方面则往往拥有丰富的相似空间(如”猫”,”狗”共有”具备皮毛”, “四条腿”等特征,仅仅在人为语义方面具有区别)。
分布式表示与非分布式表示算法的区别可以由下图进行区分:
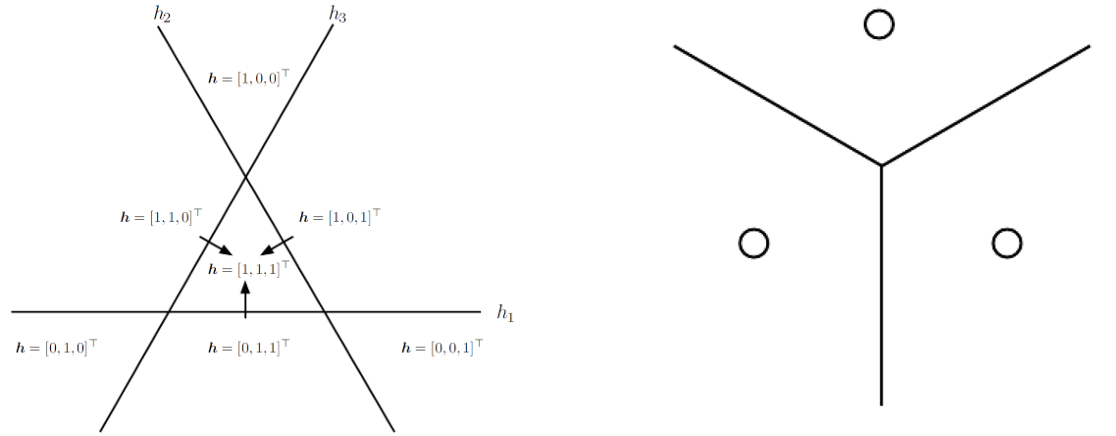
左图是分布式表示算法, 它类似于一种多标签算法,能够允许多个概念的组合(如区别有眼镜的男人和有眼镜的女人),而右图是最近邻算法(kNN)的划分空间,它不允许若干个概念的组合,只允许概念之间的多分类。如k-means,kNN,decision tree算法等都是非分布式表示算法。
分布式表示算法的好处是可以独立的学习概念本身,比如自然图像中往往会出现几个常见概念的组合(穿红衣服的人,有皮毛的动物),这种特征的组合是稀疏的(穿红衣服的动物与有皮毛的人则不会出现),如果我们采用非分布式学习方法,则会令很多神经元因为没有学习样本而空置,分布式表示学习允许我们利用稀疏的组合独立地学习各个层次的特征。
然而注意到分布式学习的缺点是我们无法学习到XoR操作(异或操作), 因为它的空间中并没有包含$[0,0,0]$的位置,这也就意味着模型无法学习到包含在数据集”信息之外”的分类特征,即如果一个测试样本不含有训练集中的任何特征,我们将无法对其输出一个类似于$[0,0,0]$的标签,这与迁移学习中零次学习的前置要求”学习器已经习得了能够表示该类任务的额外信息”相互呼应,同时也解释了为什么深度学习需要大规模数据集才能取得良好的泛化结果这个问题。
一些常用的meta prior
行文至此,我们已经回顾了从PCA到表示学习的整个发展历程,并衍生出诸如稀疏性,收缩性,线性,因子独立性等方法对表示空间进行约束,这些约束赋予模型额外的信息,我们称之为meta prior。现在,我们将这些meta prior进行总结与拓展,罗列十一种常用的meta prior如下:
-
平滑性
平滑下约束即令$\mathbf{f(x+\epsilon d)}\approx \mathbf{f(x)}$, 也就是以$\nabla_{\mathbf{X}}\mathbf{h}$梯度作为正则
-
线性
很多算法假定一些变量之间的关系是线性的,以线性回归模型为例。线性模型假设的好处是它可以对一些离观测数据较远的点也做出预测,同时线性模型一般也会满足平滑性约束。
-
多个解释因子
生成模型可能会假设数据由多个解释因子所生成,同时我们的预测目标往往和这些解释因子之间有密切的联系,即此时“用$\mathbf{h}$对$\mathbf{y}$进行预测将是高效且容易的”
-
因果因子
正如我们上文所讨论的,生成模型中$\mathbf{X}$是结果,而$\mathbf{y}$则是原因,这种因果关系的好处在于模型$p(\mathbf{X\vert y})$对于$p(\mathbf{y})$的形式是鲁棒的(因为此时$\mathbf{p(y\vert X)=p(y)}$),从而可以忽视在数据集中$p(\mathbf{y})$先验发生强烈波动后的影响。
-
深度,或者解释因子的层次组织
深度架构使得因子以某种抽象层次组织起来,从而形成抽象级别不同的层次结构
-
任务间的共享表示
即迁移学习中关于相同的输入$\mathbf{X}$,我们一般认为不同任务都可以依赖于相同的表示进行微调
-
流形假设
高维观测数据$\mathbf{X}$位于一个镶嵌在高维空间中的低维流形上,可以通过一组低维潜变量$\mathbf{h}$所变换而来,细节见流形定义与假设
-
聚类特征
如图所示,我们基于流形假设,认为高维观测数据$\mathbf{X}$位于好几个在高维空间中的低维流形上,不同的流形对应于不同的类别,流形之间并不联通。这种meta prior将使得模型聚集于图像关系以及聚类特征方面,并习得良好的聚类结果。
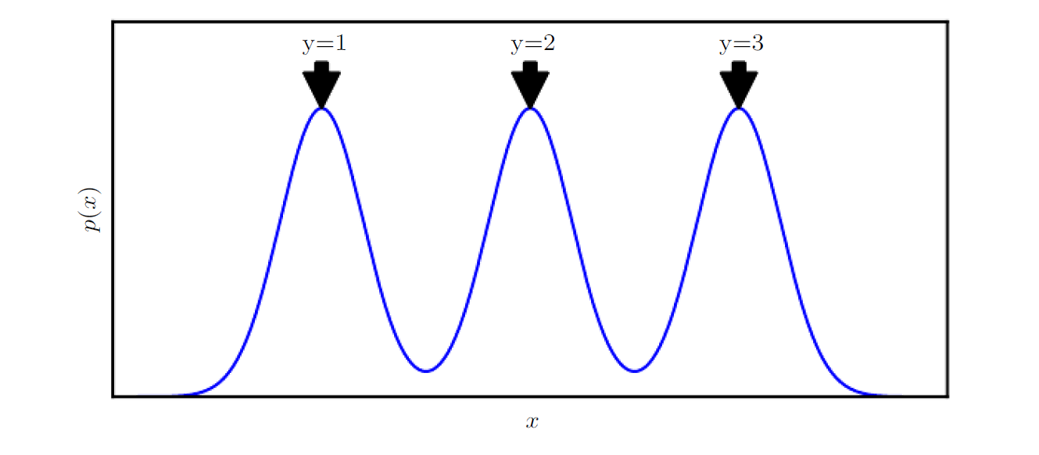
-
因子独立性
我们对因子施加独立性假设可以使得因子习得边缘独立的分布,独立性假设对于潜变量而言是常用假设
\[\mathbf{P(h)}=\Pi_{i}P(h_i)\] -
稀疏性
对因子施加先验分布
\[p(h_i)=\frac{\lambda}{4}e^{-\frac{1}{2}\lambda \vert h_i \vert}\]我们就得到了稀疏正则化项$\lambda\sum_{i} \vert h_i \vert$
-
时间与空间相关性
慢特征分析假设对于整个时序场景而言,构成整个时序场景主要语义的特征变化是缓慢的,因此我们可以用该缓慢变化构造正则化条件,具体参考Section.2中的不变特征(慢特征)分析一节
Section.4 变分推断与变分自编码器(VAE)
在之前的章节中,我们探究了表示学习的基本概念以及一些经典表示学习算法,本节中,我们将表示学习与变分推断关联起来,阐述受表示学习启发的变分推断模型的基本形式,以及参数推断的优化方法的变迁。关于变分自编码器(VAE)部分,我们将只关注于它的一些工程问题,模型的不足之处与亟待解决的问题,VAE的细节可以参考Hierarchical VAE以及A tutorial to VAE这两篇Blog,这里我们默认读者已经对VAE有了初步的了解。
表示学习模型往往呈现生成模型的形式,我们认为观测数据$\mathbf{X}$由多个解释因子$\mathbf{h}$所生成,它们具有因果性,$\mathbf{X}$是结果,而$\mathbf{h}$则是原因。模型基于$p(\mathbf{X})$的极大似然原则,利用公式
\[\mathbf{p(X)=\sum_{h}p(X,h) = \sum_{h}p(X\vert h)p(h)} \tag{9}\]对模型进行推断,推断一般需要对$p\mathbf{(X\vert h)}$以及$p(\mathbf{h})$的分布做出假设。回顾上文,如果我们对$p(\mathbf{h})$做出了Laplacian假设的话,那么会得到一个稀疏约束。
注意如果我们要给出$(9)$式的精确值,那么我们需要多次重复计算$\mathbf{p(X\vert h)}$,如果$p(\mathbf{h})$是一类连续分布的话,计算次数将趋向于无穷,这显然是不可接受的。一个非常自然的想法是,如果我们能找到出现概率最大的$\mathbf{h^{\star}}$,并利用$\mathbf{h^{\star}}$来预测 $(9)$ ,即
\[\mathbf{h^\star}=\arg\max_{\mathbf{h}}p(\mathbf{h\vert X})\]但是对于$p(\mathbf{h\vert X})$的具体形式我们仍然无法进行计算,一个方法是用预先给定的一类分布族$q(\mathbf{h\vert X})$来逼近$p(\mathbf{h\vert X})$,这样就引出了变分推断的核心公式(证据下界,变分自由能)
\[L(\mathbf{X,\theta},q)=\log p(\mathbf {X;\theta})-\mathcal{D}_{KL}[q(\mathbf{h\vert X})\Vert p(\mathbf{h\vert X;\theta})]\\ =E_{\mathbf{h\sim}q}[\log p(\mathbf{h,X})]+H(q)\\ =E_{\mathbf{h\sim}q}[\log p(\mathbf{X\vert h})]-\mathcal{D}_{KL}[q(\mathbf{h\vert X )\Vert p(h)})] \tag{10}\]与自动编码器建立联系的一个例子是,如果我们认为$q(\mathbf{h\vert X )}$满足Dirac分布
\[q(\mathbf{h\vert X}) = \delta(\mathbf{h-\mu})\]那么此时模型退化到自动编码器,即
\[\max_{\theta} \log(\mathbf{p(X\vert h=\mu)})\]变分推断的优化方法
EM算法
在早期的变分推断方法中,我们往往将$(10)$视作是一个目标函数,同时采用EM算法完成迭代优化任务。EM算法是一个用于因变量推断的优化算法。令$\mathbf{X}$表示可观测变量集,$\mathcal{h}$表示隐变量集,$\theta$表示模型参数。如果我们要对$\theta$进行极大似然估计,那么我们可以最大化已观测变量的对数似然函数来对模型参数$\theta$进行优化:
\[\log p(\mathbf{X}\vert \theta) = \log \sum_{\mathbf{h}}p(\mathbf{X,h}\vert \theta) \tag{11}\]假定待观测参数的初始值为$\theta^0$,EM算法分两步进行迭代:
-
计算期望 给定参数后,$p(\mathbf{X,h}\vert \theta)$ 变成了可以进行计算的部分,此时我们可以给出$(11)$的估计
\[Q(\theta\vert \theta^t) = E_{\mathbf{h\vert X,\theta^t}} \log p(\mathbf{X,h}\vert \theta) \tag{12}\] -
最大化$(12)$式所表达的期望
\[\theta^{t+1} = \arg \max_{\theta} Q(\theta\vert \theta^t)\]
变分法
求期望的过程是一个积分过程,因此对$(10)$的最大化可以转化为对$q$求变分的过程。我们首先介绍一下变分法的基本公式与应用,再揭示一下在$(10)$中应用变分法可以得到怎样有趣的结果。
函数$f$的函数$J[f]$称为泛函,从函数到实数的常用映射是积分,因此变分法的基本公式是
\[J[f] = \int L(x,f(x),\nabla f(x))\ dx\] \[\frac{\partial J[f]}{\partial f} = \frac{\partial L}{\partial f} - \nabla \frac{\partial L}{\partial \nabla f(x)} \tag{13}\]我们给出变分法的一个应用。考虑寻找一个定义于$x\in \mathcal{R}$上的有最大微分熵的概率密度函数$p$,其微分熵$H[p] = -\int p(x)\log p(x) dx$。我们一般不能简单地最大化$H[p]$,因为这样结果可能不是一个归一化的概率分布。同时,当方差增大的时候,熵也会无限增大。最后,给定方差后,概率分布可以不断平移而保证$H[p]$不变,因此为了获得唯一解,我们需要对分布的均值进行约束,三个约束如下表示
\[\begin{aligned} \int p(x) dx=1\\ \int xp(x) =\mu\\ \int (x-\mu)^2 p(x) = \sigma^2 \end{aligned}\]我们将带约束优化问题写成拉格朗日泛函形式
\[\mathcal{L}[p] = H[p] + \lambda_1[\int p(x)dx-1]+\lambda_2 [\int xp(x)dx-\mu] + \lambda_3 [\int x^2p(x)dx -\sigma^2]\]利用$(13)$,我们令泛函导数等于0为
\[\frac{\partial L}{\partial p} = \lambda_1 +\lambda_2 x+ \lambda_3(x-\mu)^2 -(1+\log p)=0\]可以解得
\[p = \exp[\lambda_1+\lambda_2 x+\lambda_3(x-\mu)^2 -1]\]我们将$p$代入三个约束,得到
\[p=N(\mu,\sigma^2)\]这就给出了正态分布总是令微分熵最小的分布这一经典统计学结论。为了说明变分法在变分推断中的关键作用,我们给出并证明如下定理
-
如果我们对潜变量施加因子独立性假设,即$\mathbf{q(h\vert X)} = \Pi_{i} q(h_i\vert \mathbf{X})$,那么在假设
\[p(\mathbf{h}) = \mathcal{N}(\mathbf{h};0,I);p(\mathbf{X\vert h})= \mathcal{N}(\mathbf{W^Th,\sigma^2}) \tag{14}\]时,我们可以给出结论,令$(10)$取得最大值的分布$q$是各分量独立的多元正态分布。
证明:
\(\begin{aligned} E_{q}\log p(\mathbf{X;h})+H[q] &= \log p(\mathbf{X}) +\sum_{j=1}^m E_{q} \log p(h_j\vert h_{1:j-1},\mathbf{X}) -\sum_{j=1}^m E_{q}[\log q(z_j)] \end{aligned}\) 我们记$q_{h_j}=q_j$,给定$\mathbf{X,h_{-j}}$的信息,我们对$q_j$用变分法
\[\arg\max _{q_j} \mathcal{L} = \arg\max_{q_j} E_{q}[\log p(h_j\vert \mathbf{h_{-j},X})] -E_{q_j}\log(q(z_j))\]可以得到
\[q_j \propto \exp (E_{\mathbf{h_{-j}}\sim q(\mathbf{h_{-j}\vert X})}\log p(\mathbf{X,h}))\]再利用
\[p(\mathbf{h,X}) = p(\mathbf{h})p(\mathbf{X\vert h})\]以及$(14)$中的假设,我们可以得到
\[q_j = \mathcal{N}(h_j;\mu_j,\sigma_j)\]利用独立因子假设可得,令$(10)$取得最大值的分布$q$是各分量独立的多元正态分布。
反向传播算法
利用变分法所得的正态性结论,我们将对$q$的变分推断问题简化为对$q$的正态分布参数的推断问题,此时我们就可以用深度学习作为万能近似器来学习推断,并用反向传播算法训练VAE,VAE的几篇奠基性文章正是给出了训练中的反向传播梯度计算方式。
VAE的一些工程问题讨论
上文中,我们给出了从经典潜变量模型到变分推断的一些有效结论,并通过这些结论自然引导出了VAE的基本思想。但是VAE在工程实现方面仍然有诸多问题,我们主要讨论变分下界ELBO的估计问题与生成图像问题。
-
ELBO的估计问题
我们在训练过程中,往往采用最大化ELBO$(10)$的方式来间接最大化$\mathbf{X}$的似然函数。它的问题在于我们无法定量估计 $\mathcal{D}_{KL}[p\Vert q]$,即可能会存在非常复杂的后验分布$p$,使得
\[max_{q} L(\mathbf{X},\theta^*,q)\ll\log p(\mathbf{X},\theta^*)\]此时$q$完全无法拟合$p$。
这一类问题已经得到了广泛的讨论,最新的文献是Adversarial Variational Bayes - Unifying Variational Autoencoders and Generative Adversarial Networks,文献提出用对抗训练模式寻找$p$的真实分布,并给出了该训练模式下的纳什均衡点一定是$p$的真实后验分布的数学证明,从理论上一举解决了这个问题。
-
生成图像问题
VAE生成的图像往往会出现模糊的情况,这种现象的原因尚不清楚,一种可能性是模糊性是最大似然估计的一个固有效应,因为我们需要最小化$D_{KL}[q\Vert p]$,如图所示
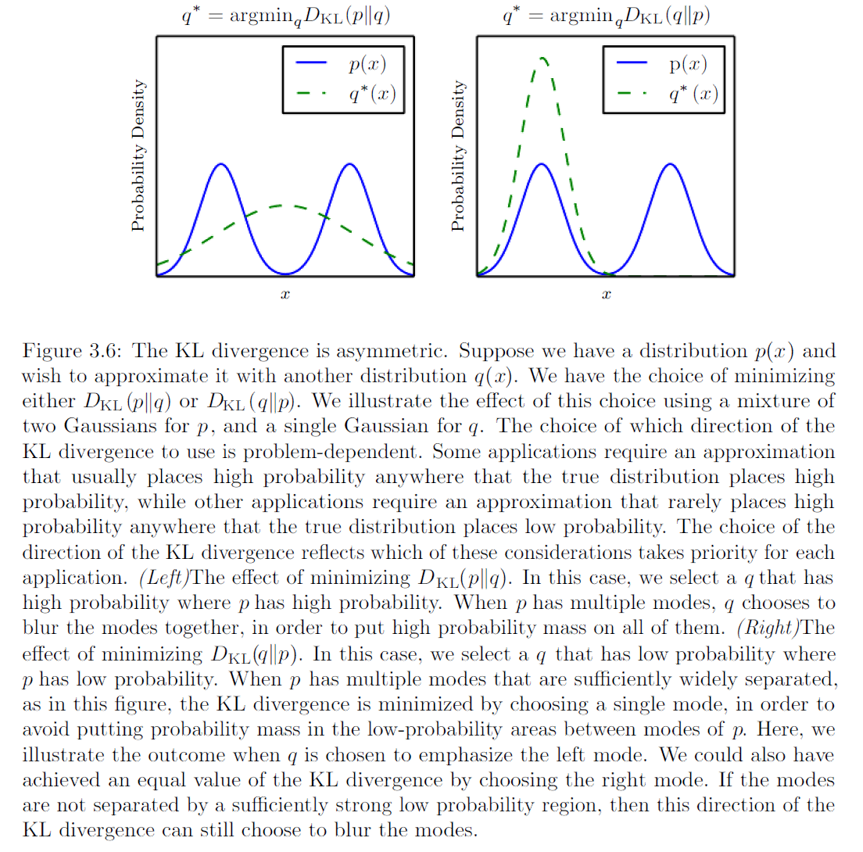
另外一个原因是因为我们对$p(\mathbf{X\vert h}$一般给出高斯分布假设,它与传统自动编码器的损失函数一致,倾向于忽略由少量像素表示的特征,或其中亮度变化微小的像素。

一个解决方法是引入GAN的对抗训练模式来训练解码器,实践证明这样的训练确实是有效的。
还有一个问题是,现代VAE模型倾向于使用完整预设潜变量空间中的较小子集,这是因为模型需要优化$\mathcal{D}_{KL}[q\Vert \mathcal{N}(0,I)]$,这使得大部分潜变量分布将退化为标准正态分布不含任何信息,而大量信息将聚集在方差极小的潜变量上,这是否是KL散度的固有问题(优化过程中将必然出现凝聚现象),还是VAE的固有问题还是一个非常值得探究的前沿方向。