- Reproducing Kernel Hilbert Space
- Domain Adaptation：各种分布距离
- Multi-Source Federated Domain Adaptation
- Reference
在A Brief Introduction to Domain Adaptation一文中，我们讨论了Domain Adaptation的数学基础和基本公式，即数据在目标域上的误差，可以由数据在源域上的经验误差，源域与目标域在特征空间上的经验距离估计，以及一个与数据量以及模型容量有关的参数来给定:
在实际应用中，$\lambda\text{与Const}$是我们无法支配的参数。现有模型思路往往是在最小化源域经验误差$\hat{\epsilon_{S}}(h)$时，构造损失函数最小化模型在特征空间上的差距$ \hat{d_{\mathcal{H}}}(\mathcal{D_S},\mathcal{D_T})$。依据对$\hat{d_\mathcal{H}}$进行度量与优化的不同方法，Domain Adaptation模型可以分为以下两类:
- 基于对抗训练的模型
- 基于MMD距离的模型
其中，前者通过优化J-S Divergency来对$\mathcal{A}-\text{distance}$作出估计，而后者则通过核方法(kernel method)构造源域与目标域分布的假设检验，计算MMD距离以估计$\hat{d}_{\mathcal{H}}(\mathcal{D}_S,\mathcal{D}_T)$。本文的主要目的是在再生希尔伯特核空间(Reproducing Kernel Hilbert Space)，依据特征空间的度量选择，构建起这些方法的联系。本文主要按以下顺序展开：首先，我们构建Reproducing Kernel Hilbert Space的相关定义，并结合Domain Adaptation的论文，介绍几个常用的Kernel。然后，我们从最基本的$\mathcal{A}-\text{distance}$概念出发，探索不同的Domain Adaptation方法所依据度量的异同，并简要介绍Wasserstein GAN的基本概念。最后，我们比较不同的Domain Adaptation方法的有效性，并顺势推导出我们组所做联邦域迁移工作的数学表达。
本文主要参考资料为
此外，我们还在叙述中引用了一些文章，我们并不完全采用它们的叙述逻辑，但是也同样在文末列出参考文献。
Reproducing Kernel Hilbert Space
在本节中，我们介绍内积，希尔伯特空间，以及再生Hilbert核空间的相关概念。在介绍这些概念之前，我们援引Gretton中的相关例子，简要介绍一下核方法以及它的重要性。
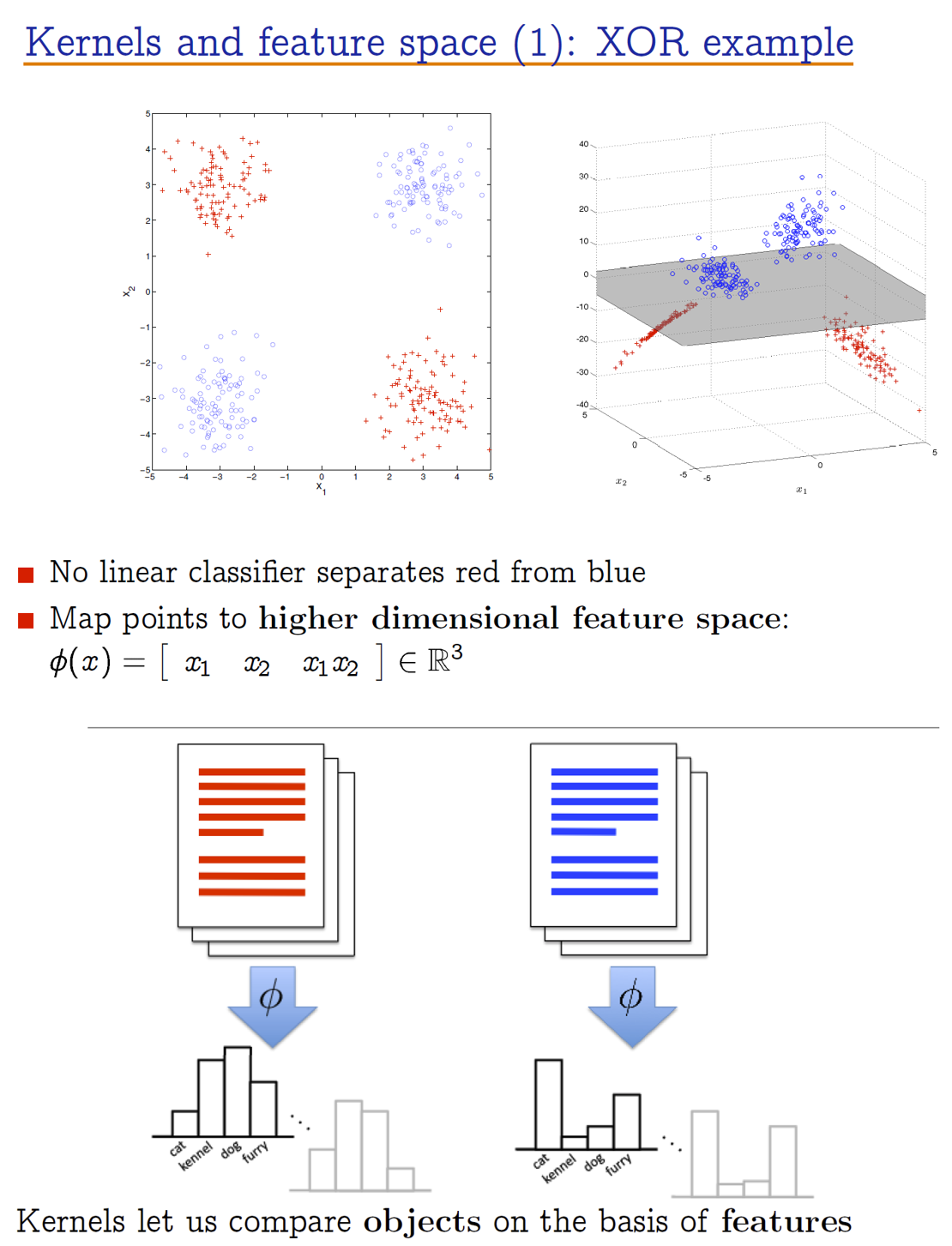
上图描述了核函数的两个例子。核函数，是一种将输入特征映射到更高维空间，以使得它在高维空间线性可分的函数。当然，也并非所有核函数都会将特征映射到更高维空间。如文本例子中采用的word-to-vector方法，将文本转化为词频向量，从而让两个本文可以区分开。因此，我们找核函数的目的，就是找到一个将输入映射到某种可分空间的函数。我们用数学语言对这种函数进行表达：
简单来说，核函数可以理解为一种距离函数，它定义了任意样本空间$\mathcal{X}$上两个样本$x_{1}, x_{2}$的”距离”，这种距离通过将样本映射到某个希尔伯特空间，然后通过计算内积得到。核方法的好处在于其对样本空间$\mathcal{X}$没有任何限定，这就给出了对离散输入数据，如图像，音频，文本等相似度计算的方法。注意到我们常用的内积一般就是逐点相乘相加，因此如果我们将$\phi(x)$展开成向量表达
那么，内积可以写成求和的形式，这种形式是非常常用的证明技巧:
\[k(x,x')=\sum_{i=1}^{p}\hat{\phi}_i(x)\hat{\phi}_i(x')\]如果核函数是无穷维的，那么只要$\Vert \phi(\cdot)\Vert_2^2\leq \infty$，我们也可以写成
\[k(x,x')=\sum_{i=1}^{\infty}\hat{\phi}_i(x)\hat{\phi}_i(x')\]给定一个核函数后，我们可以对它进行推广，简单而言，核函数相乘，相加，进行可以泰勒展开的变换，都可以得到新的核函数，即以下四条定理：
通过这四条定理，我们可以得到无数的核。比如，通过这四条定理，我们可以证明，$\exp(-\frac{\Vert x-x’\Vert_2^2}{\gamma^2})$是一个kernel，证明过程如下:
\[\Vert x-x'\Vert_2^2 = \langle x,x\rangle + \langle x',x'\rangle -2 \langle x,x' \rangle\]因此
\[\exp(-\frac{\Vert x-x'\Vert_2^2}{\gamma^2}) = \exp(-\frac{\Vert x\Vert _2^2+\Vert x'\Vert _2^2}{\gamma^2})\exp(\frac{2\langle x,x' \rangle}{\gamma^2})\]其中，对于固定的一组$\exp(-\frac{\Vert x\Vert _2^2+\Vert x’\Vert _2^2}{\gamma^2})$，我们认为它是一个常数(比如模型的正则化约束)，而$\exp(\frac{2\langle x,x’ \rangle}{\gamma^2})$是一个kernel，因此我们得到了一个指数核。
给定一个到希尔伯特空间的映射$\phi$，我们可以唯一确定一个核$k(x,x’):\mathcal{X}\times \mathcal{X} \rightarrow \mathbb{R}$。那么，如果给定一个映射$k(x,x’)$，我们是否能说它就是一个kernel呢？按照定义而言，最直觉的方法就是把kernel对应的$\phi$给挖出来。但是，这个$\phi$往往很难找，同时，一个kernel可能会对应多个$\phi$，因此，我们急需一个更简单的定理来对是否是核进行判断，这就有了正定定理：
这个定理就是说，内积一定是正定的，而对于一个函数$k(x,x’)$，如果它的Gram矩阵是正定的，那么一定可以找到一个Hilbert空间，以及一个对应的映射$\phi$，使得它是一个核。Gretton教程中，对一些著名kernel进行了分解，得到了$\phi$的坐标基形式(如$(2)$中所述)，包括基于傅里叶变换的kernel以及RBF kernel。我们上文中提到，kernel的作用是找到一个希尔伯特空间，使得该空间上的数据可分。对于RBF kernel而言，它的映射$\phi$所对应的是无穷维希尔伯特空间，那么我们选择空间的某些维度，当然就可以使得它线性可分。利用这种性质，我们可以构造一类基于核的线性映射$f(x)$，它满足
\[f(x)=\sum_{j=1}^{p}f_{j}\hat{\phi}_j(x)=\langle f,\phi(x) \rangle\]其中$f\text{是}\phi(x)$前的系数。对于这类线性映射，我们可以构造它们的回归模型为
\[\min_{f\in \mathbb{R}^p}\sum_{i=1}^{N}(y-\langle f,\phi(x) \rangle)^2+ \lambda \Vert f\Vert_2^2 \tag{3}\]而在优化过程中，我们往往可以将求$\phi(x)$这个苦差事变成求$\langle\phi(x_i),\phi(x_j)\rangle$，此时就可以直接采用计算核函数以及对应的gram矩阵来解决。注意，就算我们采用了无穷维核，即$\phi(x)\in \mathbb{R}^{\infty}$，我们的计算过程中也仍然无需触碰无穷维。以上文的核岭回归问题为例，一般我们最终计算所得的其实是每个样本所支撑的系数$\alpha_i$，即
\[f=\sum_{i=1}^{N}\alpha_i\phi(x_i)\]此时对$f(x)$的计算可以利用核函数进行，即
\[f(x)=\sum_{i=1}^N\alpha_ik(x,x_i)\]在上述基于核函数的回归问题求解中，我们发现，对每一个样本点$x$，我们可以利用核函数$k$，”再生”出一种从输入空间$\mathcal{X}$到实数域$\mathbb{R}$上的新函数：
\[k(\cdot,x)=\langle\phi(\cdot),\phi(x)\rangle:\mathcal{X}\rightarrow\mathbb{R}\]这个函数是以样本点$x$作为支撑的，而核所具有的这种性质就叫做再生性质。如果我们更广泛地考虑一类泛函空间$\mathcal{H}$，$\mathcal{H}$为非空样本集合$\mathcal{X}$到实数域$\mathbb{R}$的所有映射的空间，对于给定的核$k:\mathcal{X}\times\mathcal{X}\rightarrow\mathbb{R}$，如果这个空间满足如下性质，我们称它为Reproducing Kernel Hilbert Space，同时称$k$为这个空间的Reproducing Kernel:
- $\forall x \in \mathcal{X}, k(\cdot,x)\in \mathcal{H}$,
- $\forall x \in \mathcal{X},\forall f\in {H},f(x)=\langle f,\phi(x) \rangle$
为了方便起见，我们采用一些记号
\[f(x)=\langle f(\cdot),k(\cdot,x) \rangle_{\mathcal{H}}\]此时，我们可以将$k(x,y)$扩展到这个空间上
\[k(x,y)=\langle(k(\cdot,x),k(\cdot,y))\rangle_{\mathcal{H}}\]Domain Adaptation：各种分布距离
在第一节中，我们介绍了Kernel以及Reproducing Kernel Hilbert Space的相关概念。这些概念描述了一个故事，即样本之间可以通过核函数度量距离，而这个距离是样本在更高维空间上的投影。此外，我们可以对这个更高维空间构造平面区分样本点。而Domain Adaptation的目的则是希望模型所习得的特征”无法被区分”，我们可以用Reproducing Kernel Hilbert Space的概念构造距离完成这一目的。Domain Adaptation最原始的公式是
\[\epsilon_T(h)\leq \epsilon_S(h)+d_1(\mathcal{D}_S,\mathcal{D}_T) +\min \{\mathbf{E}_{\mathcal{D}_S}\vert f_S(\mathbf{x})-f_T(\mathbf{x})\vert,\\ \mathbf{E}_{\mathcal{D}_T}\vert f_S(\mathbf{x})-f_T(\mathbf{x})\vert \}\]其中
\[d_1(\mathcal{D}_S,\mathcal{D}_T) = 2 \sup_{B\subset \mathcal{X}}\vert \Pr_{\mathcal{D}_S}(B)-\Pr_{\mathcal{D}_T}(B)\vert\]该距离被称作为Total Variation，我们在Wasserstein Distance一章中介绍过，它具有closed form，但是需要知道分布函数的具体形式才能计算，因此，我们提出了第二种表达形式，即$\mathcal{H}-\text{distance}$以及它的变种$\mathcal{H\Delta H}-\text{distance}$
\[d_{\mathcal{H}}(\mathcal{D}_S,\mathcal{D}_T)=2 \sup_{h\in \mathcal{H}}\vert \Pr_{\mathcal{D}_S}(I(h))-\Pr_{\mathcal{D}_T}(I(h))\vert \tag{4}\] \[d_{\mathcal{H}\Delta\mathcal{H}}(\mathcal{D}_S,\mathcal{D}_T) = 2\sup_{h,h'\in \mathcal{H}}\vert E_{\mathcal{D}_S}\vert h(\mathbf{x})-h'(\mathbf{x})\vert- E_{\mathcal{D}_T}\vert h(\mathbf{x})-h'(\mathbf{x})\vert \vert \tag{5}\]这两种距离的优化目标都是$\mathcal{H}$空间上的泛函，而优化方法可以分为两类：基于对抗的方法与基于核函数的方法。
基于对抗的方法
寻找$(4),(5)$两式在Domain Adaptation场景下的最优解过程与训练对抗生成网络(GAN)是有相似性质的。首先，我们可以把(4)等价变形为
\[d_{\mathcal{H}}(\mathcal{D}_S,\mathcal{D}_T)=2 \sup_{h\in \mathcal{H}}\mathbf{E}_{x\in \mathcal{D}_S}h(x) -\mathbf{E}_{x\in \mathcal{D}_T}h(x)\]这就是Wasserstein GAN的损失函数，因此，我们可以把域迁移问题看作是一个对抗生成的过程，其输入的潜变量$z$是来自源域和目标域的不同样本，将从样本空间到分类特征空间的映射看作是生成器，然后构造判别器$h\in \mathcal{H}$，通过Min-Max训练方法令特征空间层面$\Pr(S),\Pr(T)$分布一致。用同样的方法，我们可以将$(5)$变形为
\[d_{\mathcal{H}\Delta\mathcal{H}}(\mathcal{D}_S,\mathcal{D}_T) = 2\sup_{h,h'\in \mathcal{H}} \mathbf{E}_{\mathcal{D}_S} (h(\mathbf{x})-h'(\mathbf{x}))- \mathbf{E}_{\mathcal{D}_T} (h(\mathbf{x})-h'(\mathbf{x}))\]此时，只需要构造两个分类判别器，在判别器层面让它们彼此特征远离，在生成器层面让它们的特征接近，这就是[1]中所用的思想。
基于核方法的MMD距离
在第一节中，我们介绍了核方法。简单而言，一个核对应着一个函数$\phi$，这个函数可能将低维数据映射到无穷维(RBF Kernel)，使得数据在高维空间可分。利用这一点，我们可以构造MMD距离，从而绕过不稳定的对抗部分。通过构造Reproducing Kernel Hilbert Space(RKHS)，令我的函数空间$\mathcal{H}$足够复杂，那么我就可以直接进行Min部分，直接让源域特征和目标域特征尽量接近，MMD距离就是在这种思路下导出的。
首先，我们以RKHS为基础，介绍一下kernel mean embedding的概念。对于一个给定的reproducing kernel $k(x,x’)=\langle\phi(x),\phi(x’)\rangle$，kernel mean embedding旨在给出映射$\phi$在某一数据分布函数$\mathbb{P}(x)$的”期望映射函数”：
\[\phi(\mathbb{P})=\mu_{\mathbb{P}}=\int_{\mathcal{X}}k(\cdot,x) d\mathbb{P}(x)\]注意$\phi(\mathbb{P})=\mu_{\mathbb{P}}$本身也是一个属于$\mathcal{X}\rightarrow \mathbb{R}$的映射，我们结合分布的概念，依据目标核$k(x,x’)$给出了”映射函数的期望”。这个期望当然可以通过有限数据点计算，即
\[\hat{\mu_{\mathbb{P}}}=\frac{1}{N}\sum_{i=1}^N k(\cdot,x_i)\]现在将我们的目光转向$d_{\mathcal{H}}(\mathcal{D}_S,\mathcal{D}_T)$在RKHS空间下的等价形式
\[d_{\mathcal{H}}(\mathcal{D}_S,\mathcal{D}_T) = \sup_{h\in \mathcal{H}}\mathbf{E}_{x\in \mathcal{D}_S}f(x)-{E}_{x\in \mathcal{D}_T}f(x)\tag{6}\]利用RKHS的特性
\[h(x)=\langle h(\cdot),k(\cdot,x)\rangle\]我们将$(6)$写成
\[d_{\mathcal{H}}(\mathcal{D}_S,\mathcal{D}_T)=\sup_{h\in \mathcal{H}}\langle h,\int_{X}k(\cdot,x) d\mathbb{P}_S(x)\rangle-\langle h,\int_{X}k(\cdot,x) d\mathbb{P}_T(x)\rangle\]不失一般性，我们对$h\text{加上约束}\Vert h\Vert_2^2\leq 1$，得到最终形式为
\[\text{MMD}(\mathcal{D}_S,\mathcal{D}_T)=\sup_{\Vert h\Vert_2^2\leq 1}\langle h,\mu_{\mathbb{P}_S}-\mu_{\mathbb{P}_T}\rangle\]为了利用核的性质，我们采用平方距离，即
\[\text{MMD}^2(\mathcal{D}_S,\mathcal{D}_T)=\mathbf{E}_{x,x'\sim \mathcal{D}_S}k(x,x')+\mathbf{E}_{x,x'\sim \mathcal{D}_T}k(x,x')-2\mathbf{E}_{x,x'\sim \mathcal{D}_S,\mathcal{D}_T}k(x,x')\tag{7}\][2,3]都是用$(7)$来进行的域迁移，方法都是在特征层上利用RBF Kernel计算MMD距离，计算复杂度通过一些方法可以降低到o(n)，同时，MMD距离可以纳入域适应的基本公式
\[\epsilon_{T}(h)\leq \epsilon_{S}(h)+\lambda(\epsilon_{S},\epsilon_{T}) + 2*\text{MMD}(\mathcal{D}_S,\mathcal{D}_T)+\text{Const}(d,m)\]无独有偶，MMD距离同样被用在了GAN的训练上[4]，从而取代了discriminator，但是实际效果并不好。
Multi-Source Federated Domain Adaptation
联邦域迁移领域遇到的主要问题是中间特征无法通信，这样就无法直接计算MMD距离。我们的MSFDA模型提出了利用模型中BatchNorm部分的running mean与running var来对MMD距离进行优化。
如果我们采用二次内积核，即
\[k(x,x')=(\langle x,x' \rangle+1)^2\]代入$(7)$，我们可以得到距离的等价形式为
\[\text{MMD}^2(\mathcal{D}_S,\mathcal{D}_T) =(\mathbf{E}_{\mathcal{D}_S}[x]-\mathbf{E}_{\mathcal{D}_T}[x])^2+(\mathbf{E}_{\mathcal{D}_S}[x^2]-\mathbf{E}_{\mathcal{D}_T}[x^2])^2\]即要求源域与目标域上特征的均值方差一致。我们采用的方法是，每个Client在每个训练Epoch后，采集模型中所有BatchNorm部分所得的running mean与running var，然后我们将所有Client的running mean与running var用联邦平均算法，结合我们用Shapley Value计算出的权重进行加权平均，并分发到每一个源域上。因为running mean与running var采用momentum进行更新，因此在下一个Epoch的前一半部分，模型都可以看作是固定均值方差，要求在当下的均值方差下正则化的特征仍然能减少分类任务损失。我们发现，在实际使用中，这种方法的效果很好，在效果上等价于直接计算MMD特征。
Reference
[1] Maximum Classifier Discrepancy for Unsupervised Domain Adaptation
[2] Learning Transferable Features with Deep Adaptation Networks
[3] Moment Matching for Multi-Source Domain Adaptation
[4] Training generative neural networks via Maximum Mean Discrepancy optimization