FengHZ’s Blog 首发原创
前言
我们在An introduction to Variational Autoencoders-Background,Loss function and Application中对Kingma提出的VAE进行了详细的介绍. VAE采用了潜变量假设, 将输入空间$X$与潜变量空间$Z$都看作是概率空间, 利用贝叶斯公式
\[p(x)=\int_{z}p(x\vert z)p(z)dz\]建立从潜变量空间$\mathcal{Z}$到输入空间$\mathcal{X}$分布间的映射, 并利用神经网络来拟合该映射. 在拟合过程中,我们对$p(x\vert z),q(z\vert x),p(z)$的分布进行正态性假设, 并用$q(z\vert x)$来拟合$p(z\vert x)$, 要求拟合结果要令样本点$x\in \mathcal{X}$的出现概率尽可能大,并利用Jensen不等式构造具有解析形式的变分下界
\[\log(p(x))=log(E_{q(z\vert x)}\frac{p(x,z)}{q(z\vert x)})\geq E_{q(z\vert x)}\log(\frac{p(x,z)}{q(z\vert x)})=ELBO \tag{1}\]通过最大化$(1)$中的ELBO(Evidence Lower Bound), 我们可以间接最大化$log(p(x))$, 这就是Kingma所提出VAE的基本思想. 但是, VAE将潜变量空间看作是一个随机层(Stochastic Layer), 这就会带来一些局限性. 假如流形假设为以下形式
\[x=f_1(z_1,f_2(z_2),f_2\circ f_3(z_3),\ldots,f_1\circ f_{2}\circ \ldots \circ f_{n}(z_n))\\ z_i =g_{i}\circ g_{i-1}\circ \ldots \circ g_{1}(x),i=1,2,\ldots,n\\ z_i\in \mathcal{Z},x\in \mathcal{X}\]那么潜变量之间具有较为明显的层次关系,而Kingma所提出VAE仅构建了一层随机层,此时$z_1,\ldots,z_n$的关系是并列关系, 因此没有办法揭示潜变量之间的层次关系. 基于此问题, 文献Stochastic Backpropagation and Approximate Inference in Deep Generative Models(SBAI)与Kingma同时独立提出了变分自编码器. 该文献主要有两个贡献, 一是提出了具有层次结构的变分自编码器, 二是对于重参数化技巧给出了严谨的数学证明, 是VAE领域的基石文章之一. 在该篇文章后, 也有诸多论文对Hierarchical VAE的结构与损失函数进行了优化, 如Importance Weighted Autoencoders对不同层次的因子进行了加权处理, Ladder Variational Autoencoders采用ladder结构, 将对潜变量分布的预测分为编码预测与解码预测两部分, 并用两部分预测结果的平均来作为最终预测以保证编码解码中的信息对称. Semi-supervised Learning with Deep Generative Models将Hierarchical VAE的结构扩展到半监督任务上, 将数据标签看作是服从多项式分布的离散潜变量.
本文将先给出Hiearachical VAE的基本形式与损失函数, 然后证明与重参数化技巧息息相关的几个结论,并给出从该结论出发的对于其他分布假设的计算方法, 最后对上文列出的Hierarchical VAE的扩展结构进行讨论总结.
Hierarchical VAE基本结构与损失函数
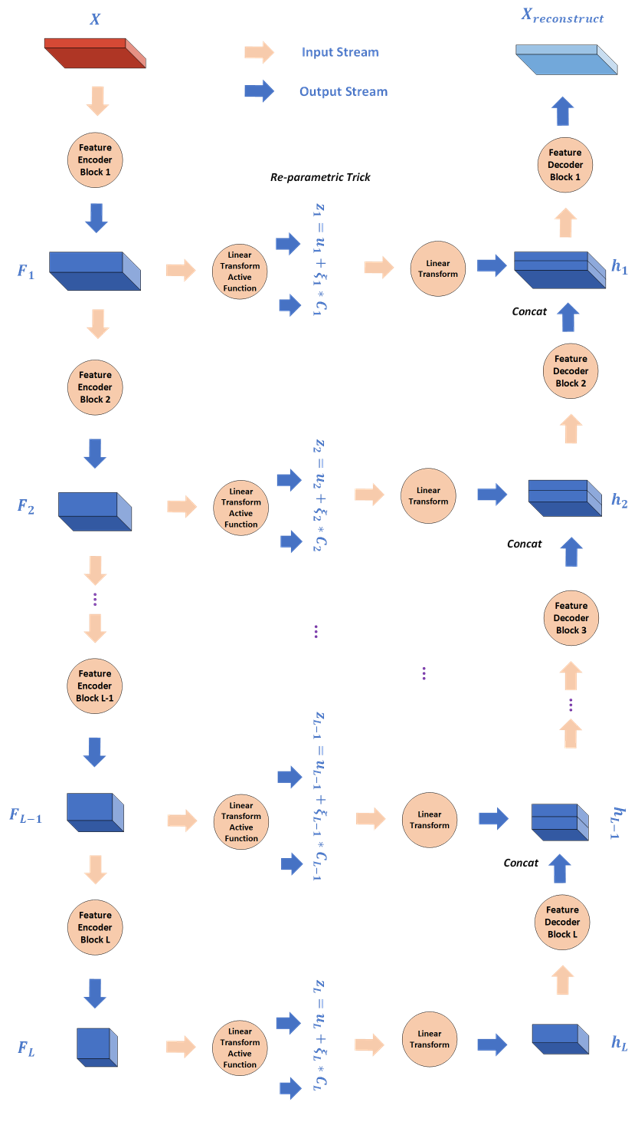
如图所示为Hierarchical VAE的基本结构,该结构与U-Net的结构非常类似, 不过U-Net是直接进行特征融合, 而Hiearachical VAE则是进行因子融合.
我们对该结构图做如下解释。首先输入生成空间中的样本$X\in \mathcal{X}$, 我们用$L$个层次排列的Feature Encoder Block来进行特征提取, 得到层次特征$F_1,F_2,\ldots,F_L$(一般认为用于图像处理的卷积神经网络低层特征提取形状信息, 高层特征提取语义信息), 然后再用相应的层次特征$F_i$对当前层次的潜变量$z_i$的分布$p(z_i\vert X) \sim \mathcal{N}(\mu_{i},C_{i})$进行推断, 得到层次潜变量$z_1,z_2,\ldots,z_L$, 然后通过这些层次潜变量构建解码器来对$p(X\vert z_1,z_2,\ldots,z_L)\sim \mathcal{N}(X,\sigma^2)$进行推断. 编码过程中我们需要对$L$组潜变量的分布进行推断, 而解码过程中我们需要对$L$组潜变量分别采样并进行分层解码.
与Kingma的VAE有所不同, 基于层次结构的VAE在原有假设基础上基于Bayes链式法则进行了扩展, 记左边的推断网络参数为$\theta^r$, 右边的生成网络参数为$\theta ^g$, $z=(z_1,\ldots,z_L),h=(h_1,\ldots,h_L)$, 其基本假设如下
\[p(\theta^g)\sim \mathcal{N}(0,\kappa I);\\ p(z_i)\sim \mathcal{N}(0,I),i\in {1,\ldots,L};\\ p(z)=\Pi_{i=1}^L p(z_i);\\ q(z_i \vert X,\theta^r)\sim \mathcal{N}(\mu_i,C_i),i\in {1,\ldots,L};\\ q(z \vert X,\theta^r)=\Pi_{i=1}^L q(z_i \vert X,\theta^r);\\ p(X,z)=p(X\vert h_1(z_{1,\ldots,L},\theta^g))p(\theta^g)\Pi_{i=1}^L p(z_i);\\ p(X,h)=p(X\vert h_1,\theta^g)p(h_{L}\vert \theta^g)p(\theta^g)\Pi_{l=1}^{L-1}p_{l}(h_l\vert h_{l+1},\theta^g);\\ p(X\vert h_1,\theta^g)\sim \mathcal{N}(g(h_1),\sigma^2)\]注意
\[p(X,h)=p(X\vert h_1,\theta^g)p(h_{L}\vert \theta^g)p(\theta^g)\Pi_{l=1}^{L-1}p_{l}(h_l\vert h_{l+1},\theta^g)\] \[p(X,z)=p(X\vert h_1(z_{1,\ldots,L},\theta^g))p(\theta^g)\Pi_{i=1}^L p(z_i)\tag{1}\]考虑到
\[z_i \sim \mathcal{N}(\mu_i,C_i),i\in {1,\ldots,L}\\ h_{L}=G_Lz_L\\ h_i=Decoder_{i+1}(h_{i+1})+G_iz_i,i\in {1,\ldots,L-1}\\\]其中$G_L$为一个线性矩阵, 这两个式子在我们的模型中是等价的,其中
\[p_l(h_l\vert h_{l+1},\theta^g) = N(Decoder_{i+1}(h_{i+1})+G_i\mu_i,G_iC_iG_i')\]我们一般使用$p(X,z)$公式以获得显式的结果, 利用如上假设, 我们对Hierarchical VAE的损失函数进行推导如下
\[\log(p(X))=\int_{z}q(z\vert X,\theta^r)\log(p(X))dz=\int_{z}q(z\vert X,\theta^r)\log(\frac{p(X,z)}{q(z\vert X,\theta^r)}\frac{q(z\vert X,\theta^r)}{p(z\vert X)})dz\\ =\int_{z}q(z\vert X,\theta^r)\log(\frac{p(X,z)}{q(z\vert X,\theta^r)})dz+\mathcal{D}[q(z\vert X,\theta^r)\Vert p(z\vert x)]\]其中
\[\int_{z}q(z\vert X,\theta^r)\log(\frac{p(X,z)}{q(z\vert X,\theta^r)})dz\tag{2}\]即为我们的目标损失函数, 也是层次潜变量下的ELBO, 我们给出在假设下代入$(1)$
\[\int_{z}q(z\vert X,\theta^r)\log(\frac{p(X,z)}{q(z\vert X,\theta^r)})dz=\int_{z}q(z\vert X,\theta^r)\log(\frac{p(X\vert h_1(z_{1,\ldots,L},\theta^g))p(\theta^g)\Pi_{i=1}^L p(z_i)}{q(z\vert X,\theta^r)})dz \\ =E_{z\sim q(z\vert X,\theta^r)}\log(p(X\vert h_1(z_{1,\ldots,L},\theta^g))+\log(p(\theta^g))-\mathcal{D}[q(z\vert X,\theta^r),p(z)]\]其中, 因为$z_1,z_2,\ldots,z_L$彼此不相关, 因此$p(z_1,\ldots,z_L) \sim \mathcal{N}(0,I),dim(I)=\sum_{l=1}^L dim(z_l)$, 同时
\[q(z\vert X,\theta^r)\sim N((\mu_{1,1},\ldots,\mu_{1,dim(z_1)},\ldots,\mu_{L,1},\ldots,\mu_{L,dim(z_L)}), \begin{pmatrix} C_1 & \\ & C_2 & \\ &&\ddots \\ &&& C_L \end{pmatrix} )\]因此
\[\mathcal{D}[q(z\vert X,\theta^r),p(z)]=\sum_{l=1}^L[\Vert \mu_l\Vert_2^2+Tr(C_l)-log\vert C_l\vert]+b\]其中$b$是一个固定常数, 我们用K个采样
\[(\hat{z}_1,\hat{z}_2,\ldots,\hat{z}_K)\sim q(z\vert X,\theta^r)\]来估计期望
\[E_{z\sim q(z\vert X,\theta^r)}\log(p(X\vert h_1(z_{1,\ldots,L},\theta^g))\tag{3}\]此时可以给出$(2)$的解析形式, 即目标函数为
\[arg\max_{\theta^g,\theta^r}\frac{1}{K}\sum_{k=1}^K-\frac{\Vert X- h_1(\hat{z_k},\theta^g \Vert_2^2)}{\sigma ^2} -\frac{\Vert \theta^g \Vert _2^2}{2*\kappa} + \sum_{l=1}^L[\Vert \mu_l\Vert_2^2+Tr(C_l)-\log\vert C_l\vert]\]它等价于
\[arg\min_{\theta^g,\theta^r}[\frac{1}{K}\sum_{k=1}^K\frac{\Vert X- h_1(\hat{z_k},\theta^g \Vert_2^2)}{\sigma ^2}](\text{part.1}) +(\frac{\Vert \theta^g \Vert _2^2}{2*\kappa} - \sum_{l=1}^L[\Vert \mu_l\Vert_2^2+Tr(C_l)-\log\vert C_l\vert])(\text{part.2}) \tag{4}\]重参数化技巧
如果我们用Deep Learning模型进行建模,而$\theta^r$与$\theta^g$ 分别是识别网络(或者说编码网络)以及生成网络(或者说解码网络)的参数, 那么一个很自然的问题是如何计算$\theta^r$与$\theta^g$的梯度.
注意Hierarchical VAE的结构图中,关于$\theta^r$参数的流向都汇聚到$(\mu_i(\theta^r),C_i(\theta^r)),i=1,2,\ldots,L$的参数预测中,$\theta^g$的参数流向也汇聚为
\[(p(X\vert h_1(z_{1,\ldots,L},\theta^g))\sim \mathcal{N}(u_{X\vert z}(h_1(z_{1,\ldots,L},\theta^g),\sigma^2)\]中对于$u_{X\vert z}$的计算, 因此计算$\theta^r,\theta^g$的梯度, 等价于计算$(4)$中损失函数对于
\[(\mu_i(\theta^r),C_i(\theta^r)),i=1,2,\ldots,L; u_{X\vert z} \tag{5}\]这些参数的梯度即可, 然后再用链式法则传导到$\theta^r,\theta^g$中.
$(4)$中的part.2部分对$(5)$的梯度计算非常简单, 因为它们都是简单线性运算, 而计算part.1部分对于$(5)$的梯度则有困难之处, 原因有两点
- $\hat{z_k}$是采样得到的, 而采样运算并不能计算梯度
-
我们用采样方法对$(3)$进行估计, 用采样方法可以对$3$的梯度进行估计吗? 即
\[\nabla_{\theta^r} E_{z\sim q(z\vert X,\theta^r)}\log(p(X\vert h_1(z_{1,\ldots,L},\theta^g)) =E_{z\sim q(z\vert X,\theta^r)} \nabla_{z} \log(p(X\vert h_1(z_{1,\ldots,L},\theta^g))\tag{6}\]是否成立, 或者说,在哪些分布假设下成立。如果成立的话, 我们自然可以用采样来估计梯度.
文献Stochastic Backpropagation and Approximate Inference in Deep Generative Models的另外一大贡献就是讨论了在正态分布与指数分布族下$(6)$式的形式(当然证明过程也是照搬前人数学家的结论), 从而诱导出了重参数化技巧, 文章给出了正态分布族与指数分布族下$(6)$式的成立条件.
正态分布族
在正态分布族上主要有两个主要结论
\[\nabla_{\mu_i}E_{z_i\sim \mathcal{N}(\mu_i,C_i),i=1,2,\ldots,L}[f(z_1,\ldots,z_L)]=E_{z_i\sim \mathcal{N}(\mu_i,C_i),i=1,2,\ldots,L}[\nabla_{z_i}f(z_1,\ldots,z_L)] \tag{7}\] \[\nabla_{C_{i,j}}E_{z_i\sim \mathcal{N}(\mu_i,C_i),i=1,2,\ldots,L}[f(z_1,\ldots,z_L)]=\frac{1}{2}E_{z_i\sim \mathcal{N}(\mu_i,C_i),i=1,2,\ldots,L}[\nabla^2_{z_i,z_j}f(z_1,\ldots,z_L)] \tag{8}\]它们的证明放于附录中, 证明用了简单的分部积分方法. 此时我们解决了对于期望的估计问题(即求导和期望符号算符在正态分布假设下可以进行交换), 但是注意到此时$(8)$式需要求$\nabla^2_{z_i,z_j}$, 这就意味着运算为$O(n^3)$, 同时梯度的流向并不自然, 因此此时我们可以引入变换
\[z=\mu + R\epsilon,s.t.\ C=RR^T,\epsilon \sim \mathcal{N}(0,I)\]此时
\[\nabla _R E_{\mathcal{N}(\mu,C)}f(z)=\nabla_R E_{\epsilon\sim \mathcal{N}(0,I)}[f(\mu+R\epsilon)]\\ =E_{\epsilon\sim \mathcal{N}(0,I)}[\epsilon g^T] \approx \sum_{k=1}^K \frac{\epsilon_ig_i^T}{K}\tag{9}\] \[\nabla _\mu E_{\mathcal{N}(\mu,C)}f(z)=\nabla_\mu E_{\epsilon\sim \mathcal{N}(0,I)}[f(\mu+R\epsilon)]\\ =E_{\epsilon\sim \mathcal{N}(0,I)}[g] \approx \sum_{k=1}^K \frac{g_i}{K}\tag{10}\]其中$g$为$f$在$\mu+R\epsilon$处的导数. 而$z=\mu + R\epsilon$的过程就是重参数化的过程, 它使得原本无法与$\mu_i,C_i$直接建立联系的采样过程变得可计算导数, 同时把对期望求导转换为对有限个采样求导并对期望进行估计的过程.
注意到$(7)$告诉我们, 我们也可以直接对$z \sim \mathcal{N}(\mu,C)$ 进行采样, 同样可以通过对采样$\hat{z_i}$进行求导而得到对$\mu$的求导.
总之, $(7),(8)$以及衍生出的$(9),(10)$都解决了如何对采样过程进行求导的问题, 基于这两组公式, 我们大可以对采样过程写forward 和 backward两个函数, 或者更简单地, 采用
\[z=\mu + R\epsilon\]这一公式直接建立forward联系,再自动进行backward即可, 以上就是重参数化技巧的意义与工程实现.
正态分布中协方差矩阵的分析
我们在上文中通过$C=RR^T$的形式给出了对协方差矩阵$C$进行推断的梯度下降法, 但是协方差矩阵仍然存在参数量过大的问题. 我们当然可以对$C$做出对角矩阵假设, 但是这样后验分布也就彼此不相关了, 无法体现因子之间的交互影响. 为了改进对角矩阵假设的缺点, 同时又不引入太多参数, 我们采用rank-1矩阵假设并辅以对角修正. 给定向量$u,d$, 记$D=diag(d)$, 我们给定协方差矩阵$C$的形式为
\[C^{-1}=D+uu^T\]这种表示能够允许在一个主要方向上高斯分布的坐标旋转, 同时只引入了少量额外参数, 在这种表示下, 我们可以给出$C$与$R$的精确形式
\[C=D^{-1}-\eta D^{-1}uu^TD^{-1}\\ \eta = \frac{1}{u^TD^{-1} u+1}\\ R=D^{-\frac{1}{2}}-\frac{1-\sqrt{\eta}}{u^TD^{-1}u}D^{-1}uu^TD^{-\frac{1}{2}}\]同时此时有
\[\log(\vert C \vert )=\log\eta-\log(\vert D \vert)\\ Tr(C)=Tr(D^{-1})-\eta u^TD^{-2}u\]指数分布族
如果有参数分布族$\mathcal{F}={p(\xi;\theta):\theta \in \Theta}$, $p(\xi;\theta)$为分布的密度函数或分布列, 如果$p(\xi;\theta)$可以表示为如下形式
\[p(\xi;\theta)=c(\theta)exp\{\sum_{j=1}^{k}Q_{j}(\theta)T_{j}(\xi)\}h(\xi)\]那么称该分布为指数分布族, 对于很多指数型分布族, 往往能找到一个函数$B(\xi;\theta)$满足
\[\nabla_{\theta}E_{p(\xi\vert \theta)}[f(\xi)]=-E_{p(\xi\vert \theta)}[\nabla_{\xi}[B(\xi;\theta)f(\xi)]] \tag{11}\]$(11)$的证明我们放于附录中, 这里贴出原论文中几个重要分布$B(\xi;\theta)$的解析形式
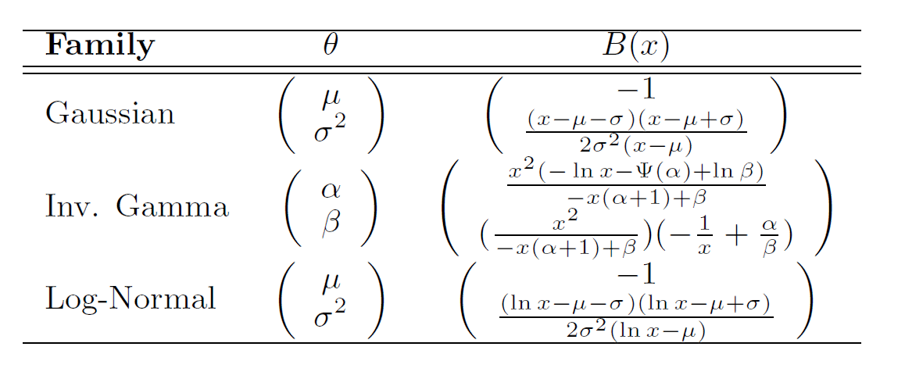
Hierarchical VAE模型结构汇总
Importance Weighted AutoEncoders
SBAI率先提出了Hiearachical VAE的基本结构与损失函数, 但是它没有解决两个问题:
-
对于层次VAE不同层次的因子, 我们认为它们之间没有相关关系,这一假设其实非常强, 同时也不自然
-
注意我们对$(3)$式期望进行估计时, 采用了随机采样K个并对这K个采样求平均作为对期望的估计, 这种估计方法对采样施加了相同的权重, 如果能对不同的采样自动赋以不同的权重则可以加入attention机制辅助训练
本篇文章就是从这两点出发, 提出了对不同的采样赋以不同权重的加权层次VAE, 同时对不同层次的因子间关系进行建模并给出了损失函数, 它的基本结构如图所示
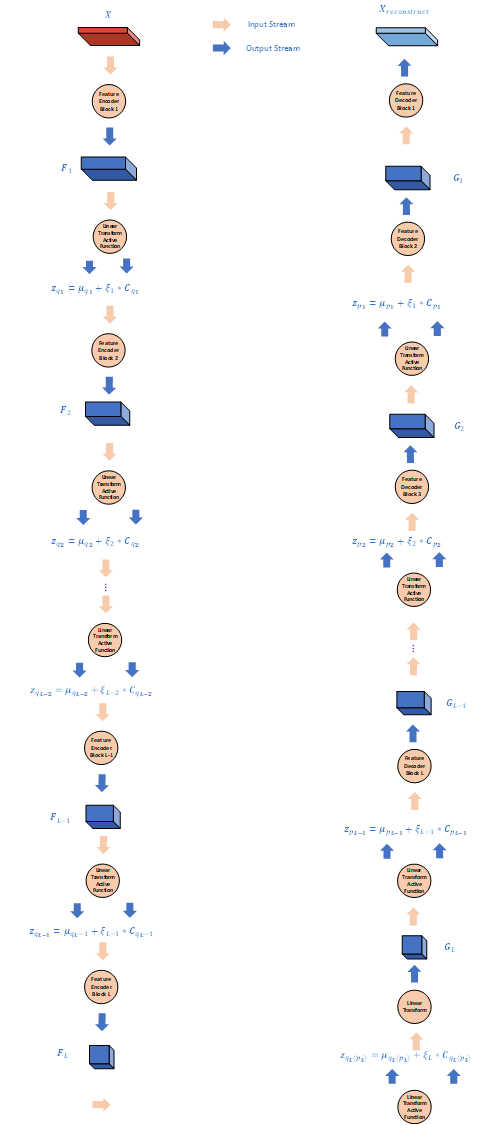
同时, 记观测空间为$\mathcal{X}$, 潜变量空间为$\mathcal{Z}$, 记$X\in \mathcal{X},z=(z_1,\ldots,z_L)\in \mathcal{Z}$, 我们对潜变量的先验后验做出以下假设
\(p(X\vert z;\theta^g)\sim \mathcal{N}(g(z_1;\theta^g),\sigma^2)\\ p(z_1,\ldots,z_L\vert \theta^g)=p(z_L\vert \theta^g)p(z_{L-1}\vert z_L,\theta^g)\ldots p(z_1\vert z_2,\theta^g)\\ q(z_1,\ldots,z_L\vert X,\theta^r)=q(z_1 \vert X,\theta^r)q(z_2\vert z_1,\theta^r)\ldots q(z_L\vert z_{L-1},\theta^r)\\ p(z_{l}\vert z_{l+1},\theta^g)\sim \mathcal{N}(\mu_{p,l},\Sigma_{p,l})\\ q(z_{l}\vert z_{l-1},\theta^r)\sim \mathcal{N}(\mu_{q,l},\Sigma_{q,l}) \tag {IWA-Hypothesis}\\\) 这样就把潜变量之间的关系刻画出来了, 而此时损失函数的推导可以写成
\[\log p(X)=\log E_{q(z\vert X)}\frac{p(X,z)}{q(z\vert X)}\geq^{\text{Jensen Inequality}}E_{q(z\vert X)}\log \frac{p(X,z)}{q(z\vert X)}=\mathcal{L}(X)\]$\mathcal{L}(x)=\log p(X)-\mathcal{D}[q(z\vert x)\Vert p(z\vert x)]$称作变分下界(ELBO), 我们通过最大化$\mathcal{L}(x)$来最大化原函数, 即目标函数为
\[arg \min _{\theta^r,\theta^g} E_{q(z\vert X,\theta ^r)}\log \frac{p(X,z\vert \theta^g)}{q(z\vert X,\theta^r)} \tag{IWA-1}\]同时,我们采用重参数化技巧, 记从$\mathcal{N}(0,I)$中采样得到$L$ 个 $\xi =(\xi _1,\ldots , \xi _L)$,并用它们生成了$z=(z_1,\ldots,z_L)$, 式(IWA-1)对参数的导数可以写成
\[\nabla _{\theta} E_{q(z\vert X,\theta ^r)}\log \frac{p(X,z\vert \theta^g)}{q(z\vert X,\theta^r)} = \nabla _{\theta} E_{\xi_1,\ldots,\xi_L \sim \mathcal{N}(0,I)}[\log \frac{p(X,z(\xi,X,\theta)\vert \theta)}{q(z(\xi,X,\theta)\vert X,\theta)}]\\ =E_{\xi_1,\ldots,\xi_L \sim \mathcal{N}(0,I)} \nabla _{\theta}[\log \frac{p(X,z(\xi,X,\theta)\vert \theta)}{q(z(\xi,X,\theta)\vert X,\theta)}]\approx \frac{1}{K}\sum _{j=1}^{K}\nabla_{\theta}\log w(X,\xi^j ,\theta)\]注意流程的推导应用了积分求导互换这一非常物理的技巧, 其中
\[w(X,\xi^j ,\theta) = \frac{p(X,z(\xi^j,X,\theta)\vert \theta)}{q(z(\xi ^j,X,\theta)\vert X,\theta)}\]按照假设是可以计算的部分, 在实际工程计算中, 我们采用IWA-Hypothesis把它写成
\[w(X,\xi^j ,\theta) = \frac{p(X\vert z_1(\xi^j,\theta);\theta)p(z_L(\xi^j)\vert \theta)p(z_{L-1}(\xi^j)\vert z_L(\xi^j),\theta)\ldots p(z_1(\xi^j)\vert z_2(\xi^j),\theta)}{q(z_1 \vert X,\theta)q(z_2\vert z_1,\theta)\ldots q(z_L\vert z_{L-1},\theta)} \tag{IWA-2}\]在训练过程中, 我们生成$\xi$, 然后代入网络进行计算,并计算在给定$\xi$ 下 (IWA-2) 的值作为目标函数, 并进行多次采样来对 (IWA-1) 进行估计.
注意到这里我们解决了计算问题, 而IWA的第二个贡献就是提出了采样次数与结果的关系, 并给出了一个具有新形式的损失函数, 这个损失函数可以自然地导出对采样的加权形式
首先我们利用一个比较巧妙的变换:
\[p(X)=E_{z\sim q(z\vert X)} \frac{p(X,z)}{q(z\vert X)}=E_{z^1,\ldots,z^{K}\sim q(z\vert X)}\frac{1}{K}\sum_{k=1}^K\frac{p(X,z^k)}{q(z^k\vert X)}\]利用Jenson不等式, 我们有
\[\log p(X)=\log E_{z^1,\ldots,z^{K}\sim q(z\vert X)}\frac{1}{K}\sum_{k=1}^K\frac{p(X,z^k)}{q(z^k\vert X)} \geq E_{z^1,\ldots,z^{K}\sim q(z\vert X)} \log \frac{1}{K}\sum_{k=1}^K\frac{p(X,z^k)}{q(z^k\vert X)} =\mathcal{L}_{K}\]注意这里对标的是
\[L(X)\approx \frac{1}{K} \sum_{k=1}^{K} \log \frac{p(X,z^k)}{q(z^k\vert X)}\]我们仍然沿用上面的记号, 记
\[w(z,X) = \frac{p(X,z^k)}{q(z^k\vert X)}\]我们有
\[\nabla _{\theta} \mathcal{L}(X) = E_{z^1,\ldots,z^{K}\sim q(z\vert X)} \frac{1}{K} \sum_{k=1}^{K} \nabla_{\theta} \log w(z,X)\approx \frac{1}{K} \sum_{k=1}^{K} \nabla_{\theta} \log w(z,X) \tag{IWA-3}\] \[\nabla _{\theta} \mathcal{L}_{K}(X) = E_{z^1,\ldots,z^{K}\sim q(z\vert X)} \nabla _{\theta} \log \frac{1}{K}\sum_{k=1}^K w(z^k,X) \tag{IWA-4}\]利用
\[\nabla _{\theta} \log \frac{1}{K}\sum_{k=1}^K w(z^k,X) = \sum_{k=1}^K \hat{w_k} \nabla _{\theta} \log w(z^k,X)\\ \text{其中 }\hat{w_k}=\frac{w(z^k,X)}{\sum_{i=1}^K w(z^i,X)}\]我们可以自然推导出它的加权形式, 同时我们有
\[\log p(X) \geq \mathcal{L}_{K+1}(X) \geq \mathcal{L}_{K}(X) \\ \text {if } \frac{p(z,x)}{q(z\vert x)} \text{ is bounded, } \lim_{k\rightarrow \infty} \mathcal{L}_{K}(X) = \log p(X)\]因此, 这就构建了采样次数与预测结果的关系, 并将预测结果写成了典型的加权形式, 这就是 IWA 的精髓了.
但是我觉得这个结构好像不太实用, 真的一点都不实用, 主要是所有的随机层彼此都相关, 这样的话对第$l,l\leq L$层而言, 它的变量必然是有交互的, 因此对角化假设是真的一点点都不能用, 也就是说协方差矩阵必须是非对角矩阵.
Ladder Variational AutoEncoders
Ladder VAE 是IWA的一个改进, 注意到IWA中编码和解码的过程对相同的中间潜变量$z_{l},l=1,\ldots,L-1$进行了对$p(z_l\vert z_{l-1})$与$q(z_{l-1}\vert z_l)$的分别预测, 我们刚刚已经提到了, 这个预测并不是很自然的, 而 Ladder VAE就改变了这个不自然的过程, 它仍然沿用写成KL散度形式的损失函数, 同时沿用了SBAI的假设[即$p(z_l\vert z_{l-1})=p(z_l)\sim \mathcal{N}(0,I)$]与IWA的结构, 它用IWA编码与解码过程中对相同的潜变量$z_l$的分布参数预测
\[(\mu_{q,l},C_{q,l}),(\mu_{p,l},C_{p,l})\]取几何平均来预测编码过程中的$q(z_l\vert z_{l-1}) \sim \mathcal{N}(\mu_l,C_l)$, 即
\[C_{l_{i,j}} = \frac{1}{\frac{1}{C_{ p,l_{i,j} } }+\frac{1}{C_{ q,l_{i,j} } } }\\ \mu_{l_{i}}=\frac{\frac{\mu_{q_{i}}}{C_{q,l_{i,i}}}+\frac{\mu_{p_{i}}}{C_{ {p,l}_{i,i} } } }{\frac{1}{C_{ p,l_{i,j} } }+\frac{1}{C_{ q,l_{i,j} } } }\]并采用损失函数
\[E_{z\sim q(z\vert X,\theta^r)}\log(p(X\vert h_1(z_{1,\ldots,L},\theta^g))+\log(p(\theta^g))-\mathcal{D}[q(z\vert X,\theta^r),p(z)]\]来进行优化, Ladder VAE的好处是沿用了更加make sense的结构并同时使用了编码解码的层次信息.
Semi-supervised Learning with Deep Generative Models
本文提出了一种用Hierarchical VAE来进行半监督学习的策略, 它的结构可以看成2层IWA, 它将潜变量分为两层, 第一层仍然是符合正态性假设的潜变量, 而第二层则是由符合多项式分布的潜变量与正态潜变量构成, 其中符合多项式分布的潜变量代表着标签潜变量, 而正态潜变量则是与第一层潜变量服从相同假设的层次潜变量, 如图所示为它的结构
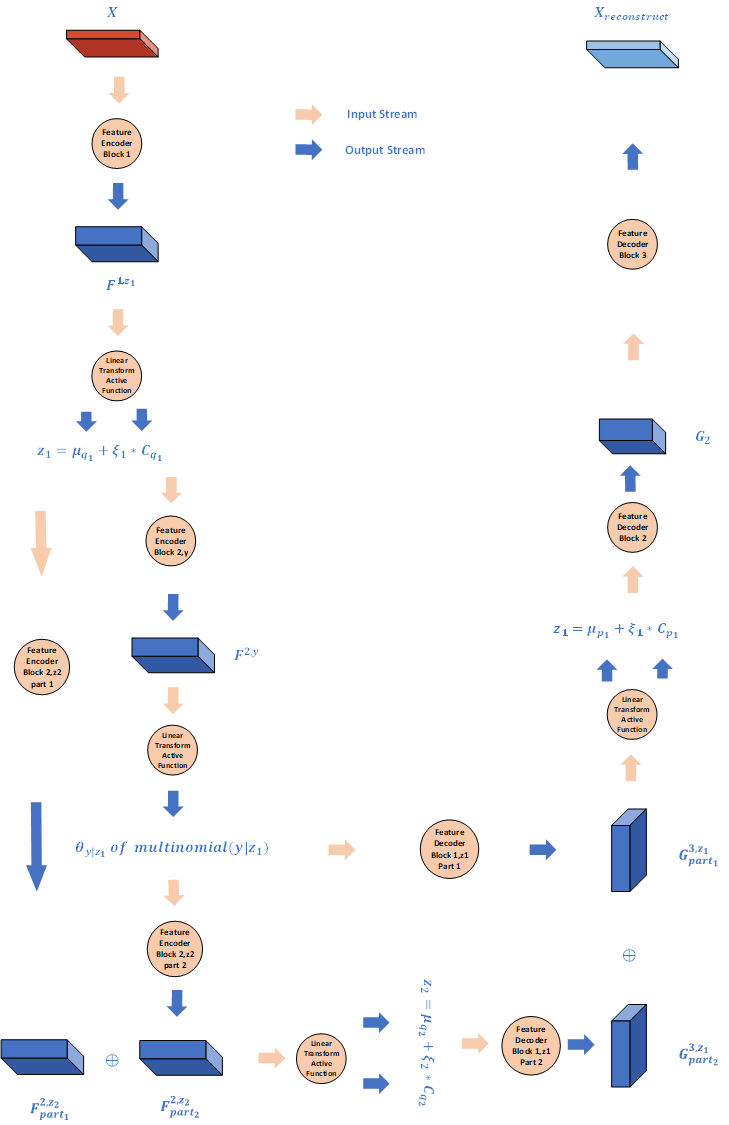
它的基本假设如下
\[p(X,y,z_1,z_2)=p(X\vert z_1)p(z_1 \vert y,z_2)p(z_2)p(y)\\ p(z_2)\sim \mathcal{N}(0,I),i = 1,2;\\ p(y)\sim \text{multinomial}(n,\theta_{prior}),n\text{ is the number of classes,$\theta$ is the prior distribution of classes}\\ p(z_1\vert y,z_2)= \mathcal{N}(\mu_{p_1},C_{p_1}) \\ q(z_1,z_2,y\vert X)=q(z_1\vert X)q(y \vert z_1)q(z_2\vert z_1,y) \\ q(z_1\vert X) \sim \mathcal{N}(\mu_{q_1},C_{q_1})\\ q(y\vert z_1) \sim \text{multinomial}(n,\theta_{pos}),n\text{ is the number of classes,$\theta$ is the posterior distribution of classes}\\ q(z_2\vert y,z_1) \sim \mathcal{N}(\mu_{q_2},C_{q_2})\]损失函数都是基于Jenson不等式而得到的, 对它的分类讨论分为两种, 一种是对有标注数据的损失, 还有一种是对无标注数据的损失.
有标注损失
对有标注数据的损失中, 我们认为$y$是一个确定变量, 即此时$p(y)$是一个退化分布, 损失函数可以写成
\[\log p(X,y)\geq E_{z\sim q(z\vert X,y)}[\log p(x\vert z_1)+\log p(z_1,z_2)-\log q(z_1,z_2\vert X,y)]\\ =E_{z\sim q(z\vert X,y)}\log p(x\vert z_1)-\mathcal{D}[q(z_1,z_2\vert X,y) \Vert p(z_1,z_2)]\\ = -\mathcal{L}(X,y)\]其中
\[\mathcal{D}[q(z_1,z_2\vert X,y) \Vert p(z_1,z_2)]=E_{q(z_1,z_2\vert X,y)}[\log\frac{q(z_1\vert X)}{p(z_1\vert y,z_2)}+ \log \frac{q(z_2\vert z_1,y)}{p(z_2)}] \\ \approx \sum_{k=1}^{K}\frac{1}{K}[\log\frac{q(z_1^k\vert X)}{p(z_1^k\vert y,z_2^k)}+ \log \frac{q(z_2^k\vert z_1^k,y)}{p(z_2^k)}]\]或者也可以写成不太恰当的粗略解析形式
\[\mathcal{D}[q(z_1,z_2\vert X,y) \Vert p(z_1,z_2)] = \mathcal{D}[q(z_1\vert x)\Vert p(z_1\vert y,z_2)] +\mathcal{D}[q(z_2\vert z_1,y)\Vert p(z_2)]\]由正态分布假设, 该形式存在解析解.
无标注损失
对于那些没有标注的损失函数而言, 我们将标注看成是一个服从多项式分布的随机变量
\[\log p(X) \geq E_{y,z\sim q(z\vert X)}[\log p(x\vert z_1)+\log p(z_1,z_2)+\log p_{\theta}(y)-\log q(z_1,z_2,y\vert X) \\ = E_{y,z\sim q(z,y\vert X)}[\log p(x\vert z_1)+\log p(z_1,z_2)+\log p_{\theta}(y)- \log q(z_1\vert X)-\log q(y \vert z_1)-\log q(z_2\vert z_1,y) ]\\ = E_{y \sim q(y\vert z_1)}E_{z_1,z_2\sim q(z_1,z_2\vert X,y)}[\log p(x\vert z_1)+\log p(z_1,z_2)+\log p_{\theta}(y)- \log q(z_1\vert X)-\log q(y \vert z_1)-\log q(z_2\vert z_1,y) ]\\ =\sum_{y}q_(y\vert z_1)(-\mathcal{L}(X,y)) +\mathcal{H}(q(y\vert z_1))=- \mathcal{U}(X)\]因此, 此时我们可以很自然地导出损失函数(用$\tilde{p_l},\tilde{p_u}$)分别表示有标注和没有标注的数据集.
\[\mathcal{J}=\sum_{X,y \sim \tilde{p_l}}\mathcal{L}(X,y) +\sum_{X \sim \tilde{p_u}} \mathcal{U}(X)\]注意到上面的所有推导都是将$y$视作为一个离散潜变量而言的, 尤其是损失函数$\mathcal{L}(X,y)$中并没有利用$y$的标注信息, 注意给定$y$后相当于$y$坍缩到一个退化分布(或者说有一个类出现概率为1的多项式分布), 因此我们再引入此时变分编码器对离散潜变量的分布预测与退化分布的KL散度,通过最小化它来利用标注信息, 即
\[\mathcal{C}=\min \mathcal{D}[p(y\vert X) \Vert q(y\vert z_1)]=\min -\sum_{y_i} y_i \log q(y_i\vert z_1)\]因此最后损失函数为
\[\mathcal{J}^{\alpha} = \mathcal{J} +\alpha \mathcal{C}\]注意, 在这种层次模型中, 应当满足的一个条件是
\[\dim(z_2)+\dim(y) \geq \dim(z_1)\]附录
$(7)-(11)$证明
-
(Bonnet’s Theorem)
令 \(f(\xi_1,\ldots,\xi_L):R^{d_1}\times R^{d_2}\times \ldots \times R^{d_L} \rightarrow R\) 为对于任意$\xi_i$可积且二次可微的函数. 给定$\xi_i \sim \mathcal{N}(\mu_i,C_i)$, 我们有以下公式成立
\[\nabla_{\mu_i}E_{\xi_l \sim \mathcal{N}(\mu_l,C_l)}f(\xi_1,\ldots,\xi_L)=E_{\xi_l \sim \mathcal{N}(\mu_l,C_l)}\nabla_{\xi_i}f(\xi_1,\ldots,\xi_L)\]证明:
\[\nabla_{\mu_i}E_{\xi_l \sim \mathcal{N}(\mu_l,C_l)}f(\xi_1,\ldots,\xi_L) \\ =\nabla _{u_i}\int_{\xi_1}\ldots\int_{\xi_L}\Pi_{l=1}^{L} \frac{1}{\sqrt{2\pi \vert C_l\vert }}\exp(-\frac{(\xi_l -\mu_l)'C_{l}^{-1}(\xi_l-\mu_l)}{2})f(\xi_1,\ldots,\xi_L)d\xi_1\ldots d\xi_L\\ =\int_{\xi_1}\ldots\int_{\xi_L}[\Pi_{\neg i} \frac{1}{\sqrt{2\pi \vert C_l\vert }}\exp(-\frac{(\xi_l -\mu_l)'C_{l}^{-1}(\xi_l-\mu_l)}{2})]\nabla _{u_i}p(\xi_i)f(\xi_1,\ldots,\xi_L)d\xi_1\ldots d\xi_L \tag{A.1}\]注意到
\[p(\xi_i)=\frac{1}{\sqrt{2\pi \vert C_i\vert }}\exp(-\frac{(\xi_i -\mu_i)'C_{i}^{-1}(\xi_i-\mu_i)}{2}) \\\]利用矩阵求导公式$\frac{\partial(Ax+b)^TC(Dx+e)}{\partial x}=D^TC^T(Ax+b)+A^TC(Dx+e)$我们有
\[\nabla_{\mu_i}p(\xi_i)=-\nabla_{\xi_i}p(\xi_i)\]代入$(A.1)$有
\[= \int_{\xi_1}\ldots\int_{\xi_L}[\Pi_{\neg i} \frac{1}{\sqrt{2\pi \vert C_l\vert }}\exp(-\frac{(\xi_l -\mu_l)'C_{l}^{-1}(\xi_l-\mu_l)}{2})]-\nabla _{\xi_i}p(\xi_i)f(\xi_1,\ldots,\xi_L)d\xi_1\ldots d\xi_L\]利用分部积分公式
\[=[-\int_{\xi_1}\ldots\int_{\xi_{L \neg i}} \Pi_{\neg i}p(\xi_l)f(\xi_1,\ldots,\xi_L)d\xi_1\ldots d\xi_{L \neg i}p(\xi_i)]_{\xi_i=-\infty}^{\xi_i=+\infty}(=0)+ \int_{\xi_1}\ldots\int_{\xi_L}\Pi p(\xi_l)\nabla _{\xi_i}f(\xi_1,\ldots,\xi_L)d\xi_1\ldots d\xi_L\\ =E_{\xi_l \sim \mathcal{N}(\mu_l,C_l)}\nabla_{\xi_i}f(\xi_1,\ldots,\xi_L)\] -
(Price’s theorem)
与Bonnet’s Theorem相同条件, 我们有以下公式成立
\(\nabla_{C_{i,j}}E_{\xi_l \sim \mathcal{N}(0,C_l)}f(\xi_1,\ldots,\xi_L)=E_{\xi_l \sim \mathcal{N}(0,C_l)}\nabla_{\xi_i,\xi_j}f(\xi_1,\ldots,\xi_L)\) 这里与Bonnet’s Theorem相同证明方法,同样用了
\[\nabla C_{i,j} \mathcal{N}(\mu,C)=\frac{1}{2}\nabla_{\xi_i,\xi_j}\mathcal{N}(\mu,C)\] -
指数分布族
对于指数分布族$p(x\vert \theta)=h(x)\exp(\eta(\theta)^T\phi(x)-A(\theta))$而言, 我们有以下公式成立
\[\nabla_{\theta}E_{p}[f(x)]=-E_{p}[B(x;\theta)\nabla_{x}[f(x)]]\]其中
\[B(x,\theta)=\frac{[\nabla_{\theta}\eta(\theta)\phi(x)-\nabla_{\theta}A(\theta)]}{[\nabla_{x}\log[h(x)]+\eta(\theta^T)\nabla_{x}\phi(x)]}\]这里仍然使用了
\[\nabla_{\theta} p(x\vert \theta) f(x)dx=\nabla_{x} p(x\vert \theta)B(x;\theta)f(x)\]这一我们之前已经用过很多次的公式