分类任务是深度学习模型的基本任务。深度学习模型的基本分类流程非常简单,输入待预测的数据,经分层提取特征,再用全连接层将特征输出为每个类的置信度,最后将置信度转化为one-hot编码。整个流程中,将置信度转化为ont-hot编码的操作一般是采用最大值方法,即选择概率最大的一类,将其值置为1,其他值置为0。在整个流程中,置信度转化过程看起来并不自然。假设一个二分类问题,如果我们预测两个输入的分类置信度分别为(0.6,0.4)和(0.99,0.01),它们的one-hot编码转化都是(1,0),但是前者的预测显然更加没有底气一些。同时注意到分类问题中,每一个输入的ground truth标签基本都为one-hot化的编码,但是网络实际输出的则是经过softmax操作的置信度,这在可解释性上也导致了一些问题。
本文主要梳理上述问题,并介绍几个可以联系置信度与转化后的one-hot编码好坏的指标,ECE。本文主要参考外文Blog:The Importance of Calibrating Your Deep Production Model。
从概率论角度联系置信度和one-hot标签
对于一个数据集$\mathcal{D}$而言,它由成对的输入-标签组成,即$(X,y)\in \mathcal{D}$。其中,$y$为输入$X$对应的标签,通常以one-hot的形式出现,如二分类问题中的$(1,0)$。假设模型函数为$\mathit{f}$,对于输入$X$,模型会给出置信概率$q$,它通常不是one-hot编码,一般形式为float数组,如$(0.89,0.11)$。对每一个样本,我们都用交叉熵计算其预测损失:
\[-(1\cdot\log 0.89+0\cdot \log 0.11)\]注意到,标签$y$是一个确定的值,并不具有什么概率意义。但是,我们计算损失的时候,是用标签$y$与置信概率$q$的对数似然直接相乘相加,这个过程应该如何从概率论的角度理解呢?这里,我们需要引入一个自然概率$p$作为从输入到标签的中间件。以明天会不会下雨的二分类问题为例。在今天,我们对明天会不会下雨的观测一般是不确定的,它有一个概率,如0.9的可能性下雨,0.1的可能性不下雨。到了明天,这个事件就成了一个确定性的是否事件了,如果下雨了,我们就打上标签$(1,0)$,这是因为我们已经进行了一次观测。如果存在多个平行宇宙,我们可以进行多次观测,总有一部分是下雨,而也有一部分是不下雨的,但是只要我们观测的次数足够多,那么下雨的次数除以总次数总是会逼近0.9。通过$p=(0.9,0.1)$ 这个中间件,我们就可以理解标签是怎么来的,即标签只是一次观测的结果,而模型所预测的是其真实概率$p$,它可以用样本的均值来得到,即
\[-p\cdot \log q =-\sum_{i=1}^{N}\frac{y_i}{N}\cdot \log q\]将求和符号拿出来,我们就得到了单个样本的交叉熵形式。在实际神经网络的训练过程中,为了计算方便,我们不断地选取batch, 然后对每个样本独立计算交叉熵再相加即可。
ECE与MEC:度量预测置信q与真实概率p的距离
在上一节中,我们梳理了从真实概率$p$,到ground truth标签$y$,以及到预测概率$q$之间的关系。在常规的模型精度检测中,我们一般用样本预测概率$q$的最大值来得到预测标签$\hat{y}$,通过比较$\hat{y}$与$y$来对模型的好坏做出判断。这种判断是实用的,但是也是很表层的。正如上文所述,即使$p,q$之间相差很大很大,它们用最大值判定得到的标签也可能完全一致。但是,在实际使用中,对于任何一个样本的$p$都是不可知的,或者是非常难以获得的。那么,如何在一个多分类模型中比较$p$与$q$的距离呢?我们可以从$q$所代表的准确率的角度考虑问题。按上文的定义,如果预测概率$q$接近于真实概率$p$,那么$q=(x,1-x)$意味着我们将样本预测为$(1,0)$,会有$100x\%$的样本预测正确,而$100(1-x)\%$的样本预测出现问题。那么我们可以通过$\hat{y}$与$y$计算准确度,并将该准确度与$q$相比,看看预测的置信度是否与准确度相似。具体而言,对于K分类问题,我们选取某一类$k$,将所有样本的预测置信度从小到大进行排序,然后划定M个区间,如$(0,\frac{1}{M}),\cdots,(\frac{M-1}{M},1)$。对于任意第m个区间$B_m$,我们将落在这个区间内的所有样本都预测为该类$k$,然后计算其与真实标签的准确度,即$\text{Acc}(B_m)$。然后,我们将该区间内的所有样本置信度相加求和,计算$B_m$区间的平均置信度
\[\text{Conf}(B_m)=\frac{1}{\vert B_m\vert}\sum_{i\in B_m}q_i\]如果$q$与$p$相差不大(这里相差不大的意思是,如果置信度是0.8,那么真实概率意义也会接近于0.8),那么$\text{Conf}(B_m)$与$\text{Acc}(B_m)$的距离也会很小,因此,对于某一类$k$,我们可以利用$\text{Conf}(B_m)$与$\text{Acc}(B_m)$,计算对于k类的期望精度误差(ECE)与最大精度误差(MCE)
\(\text{ECE}(k)=\sum_{m=1}^M\frac{\vert B_m\vert }{n}\vert \text{Conf}(B_m)-\text{Acc}(B_m)\vert\) 当$\text{ECE}(k)=0$,说明对于第$k$类而言,$q$基本与$p$完全一致。$ECE$是度量所有区间上$p$与$q$的平均差距的,但是在实际使用中,往往置信度较低与较高的区间$\vert \text{Conf}(B_m)-\text{Acc}(B_m)\vert$比较低,而中间部分区间反而比较高,这个时候,我们可以用最大精度误差来代替,同时观察哪几个区间部分的精度误差较大,在这几个区间,q的置信度不具有概率意义: \(\text{MCE}(k)=\max_{m\in \{1,...,m\}}\vert \text{Conf}(B_m)-\text{Acc}(B_m)\vert\)
降低ECE与MCE
在实验过程中,一个很显著的现象是,深度学习模型的交叉熵损失降低并不代表ECE与MEC也在降低。如下图所示,在Cifar100的loss降低的过程中,其ECE与MEC反而增加了。
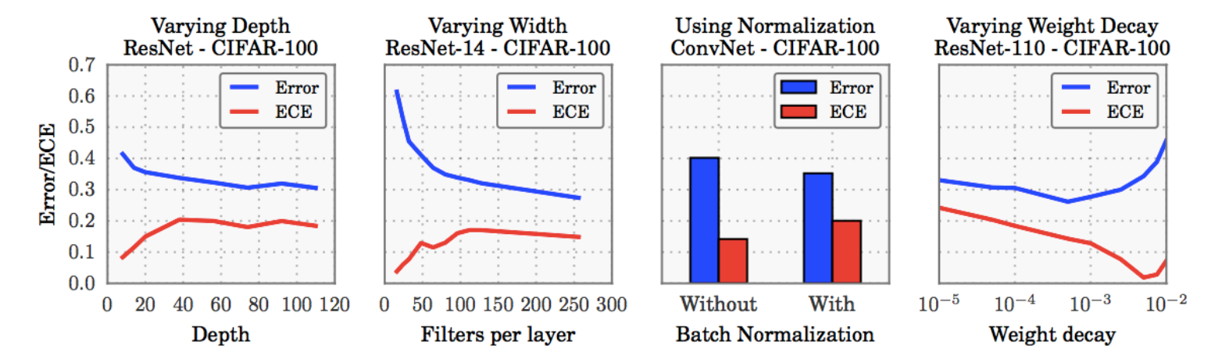
降低ECE与MEC,有两个很有用的方法,分别是为softmax增加中心化的温度系数,以及标签平滑化。这两种方法都是通过让自己的网络较为自信(预测向两端集中),同时又不至于过于自信(避免one-hot导致的极端1-0),从而增加网络对自己预测的置信度。