- 序言与笔记大纲
- 文献[1]想要解决什么样的问题
- 文献[1]本质上是想解决逐像素预测缺乏连续性的问题
- 对抗网络有什么好处呢
- 文献[1]通过什么样的系统解决了这个问题
- 文献[2]想要解决什么问题
- 关于主流的语义分割网络[3][4]
- 参考文献
报告题目: Deep Adversarial Network Reading Recordings
序言与笔记大纲
为了做关于Deep Adversarial Network的相关研究,我认真阅读了文献[1],[2],并顺带阅读了文献[3]以及文献[4]写作了这篇报告。
我的报告主要想要结合以下几个问题展开:
- 文献[1]想要解决什么样的问题
- 文献[2]在文献[1]的基础上进行了什么样的改动,并完成了什么样的问题
- 文献[1],文献[2]在解决问题的过程中遇到了什么样的困难,它们是如何解决这些困难的
- 文献[3]与文献[4]所提到的关于语义分割的主流是什么,这些部分对我的工作是否有用。
- 我的下一步工作重心与工作目的是什么
读完报告的目的应该是我从头到尾就可以把整个网络给复现出来,里面的参数设置与细节也一清二楚。
文献[1]想要解决什么样的问题
文献[1]本质上是想解决逐像素预测缺乏连续性的问题
文献[1]是采用对抗神经网络来进行语义分割的一个网络。语义分割系统长久以来一直在采用一种全卷积神经网络来进行一种端到端的训练,它输出的是pixel-wise的预测,采用的是交叉熵函数,这就导致了我们的预测是对每一个点的预测。但是语义分割是一个比较一致的任务,一般语义分割的结果在边界内部都具有连续性,而这样一个逐像素预测的性质就缺少了这种高阶的连续性。为了解决这个问题,文献[1]就提出了对抗网络来学习这种高阶连续性。
对抗网络有什么好处呢
对抗网络的本质是一个动态的损失函数。正如上文所述,逐像素预测的损失函数本质上增加了预测的负担,而逐像素预测会使得预测模糊的概率越来越大,同时减少了预测的一致性。增加对抗网络参数的损失函数将损失放在了一个高维的空间上(作为核函数),这样能体现这种一致性。
同时,有时候,一个网络分类得不好的原因人是很难知道的,也就很难批评它。但是分割图像与自然的ground truth的图像之间的差别却是一个分类器所能分出来的,在这一点上无人能及,因此对抗网络就可以有很高能力,以及在检验分割与ground truth不匹配的时候具有更高阶的判断。
文献[1]通过什么样的系统解决了这个问题
重新设计损失函数
注意到上文所说,文献[1]的本质是通过批评ground truth与segment prediction的差别,来使得loss函数变得参数化(这里也是一个非常重要的如何把损失函数参数化的思想),同时使得网络能学习一致性特征。因此本质上是把损失函数变成了三个部分: \(l(\theta_s,\theta_a)=\sum_{n=1}^Nl_{mce}(s(x_n),y_n)-\lambda[l_{bce}(a(x_n,y_n),1)+l_{bce}(a(x_n,s(x_n)),0)]\) 注意到$x_n,y_n,s(x_n)$是一组,对应着原始输入,ground truth以及分割结果。注意到这里$l_{mce}(\hat{y},y)=-\sum_{i=1}^{H\times W}\sum_{c=1}^Cy_{ic}ln\hat{y_{ic}}$,同时$l_{bce}$也就是所谓的双线性的损失。
因此,我们先训练分割模型,然后在分割模型的基础上选N组$(x_n,y_n,s(x_n))$,然后训练一个对抗网络: \(\sum_{n=1}^N l_{bce}(a(x_n,y_n),1)+l_{bce}(a(x_n,s(x_n)),0)\) 这个网络用来鉴别ground truth与segment prediction的区别。在训练好这个网络之后,我们可以训练另外一个带参数loss函数的分割网络: \(\sum_{n=1}^Nl_{mce}(s(x_n),y_n)-\lambda l_{bce}(a(x_n,s(x_n)),0)\) 这里有一个小tips,就是把$-\lambda l_{bce}(a(x_n,s(x_n)),0)$改成$\lambda l_{bce}(a(x_n,s(x_n)),1)$,也就是说我们的目的是让对抗网络区分不出来,这样loss函数就是带参数的loss函数了。
选取合适的语义分割网络
文献[3],[4]是现在最先进的语义分割网络的两篇文章,我将会在后面介绍它们
如何选取对抗网络的输入
对抗网络的输入是一个很重要的问题。我们需要让它是原图像,以及ground truth或segment prediction的函数,因此如何组织输入就是一个问题。我们大可把原图像和其中之一concate作为输入,但是这样可能导致对抗网络只采取两个之一作为评判标准。论文给出了3个输入可能的探索。
输入特征的concate
作者在斯坦福背景数据库中选择了建立两个独立的branch处理原始图像与分割label,每个取64-d的特征图,把特征图concate到一起得到输入。
直接输入分割结果
直接输入分割结果是个好主意,但是网络可能就会直接判断你分割的结果是{0,1}的还是[0,1]的来进行决策。(那如果我把预测的输出也弄成{0,1}呢?没说)
相乘
直接把分割结果与原图像相乘作为输入。这是很不错的,但如果按整数和非整数区分呢?
将ground truth做分布处理再相乘
注意到预测与gt具有整数和浮点数的区别,因此我们需要对gt也做相应的处理。假设我们分为C类,对每一类的每一个位置i,做如下处理: \(y_{il}=max(\gamma,s(x)_{il}),if\ y_{il}=1\\ y_{ic}=s(x)_{ic}*\frac{1-y_{il}}{1-s(x)_{il}},else\) 文中给出的好方法是让$\gamma=0.9$,然后相乘输入之后直接用深度卷积网络并输出参数,具体在附录中。
超参数选取
文献选用了交叉检验法来选取超参数,并用3个测度表现的数值(注意到要写多个测度表现的数值),分别为per class accuracy,per pixel accuracy,IoU,给出的参考超参数是$\lambda=2,lr=1e-3$。
文献[2]想要解决什么问题
如何利用未标注数据辅助训练
文献[2]在文献[1]的基础上进行了扩展,想要解决的问题是如何利用未标注的数据。它的网络结构基本与文献[1]没有差别,它直接通过修改损失函数来达到了这一目的,它将损失函数修改为如下表示:
$l(\theta_s,\theta_a)=\sum_{n=1}^Nl_{mce}(s(x_n),y_n)-\sum_{m=1}^M \lambda[l_{bce}(a(x_m,y_m),1)+l_{bce}(a(x_m,s(x_m)),0)]$
对抗神经网络的损失改为 \(\lambda[\sum_{n=1}^nl_{bce}(E(S(X_m),X_m),1)+\sum_{m=1}^Ml_{bce}(E(S(U_n),U_n),0)]\) 分割神经网络的损失改为 \(\sum_{n=1}^Nl_{mce}(S(X_n),Y_n)+\lambda(\sum_{m=1}^Ml_{bce}(E(S(U_n),U_n),1))\) 相当于这里我们取了N组$(X_n,Y_n,S(X_n))$与M组未标注的$(X_m,S(X_m))$,然后在对抗网络中,我们需要正确区分标注的数据的分割结果与未标注的数据的分割结果(也就是说这里不区分gt了,区分标注与未标注了,把gt改成了未标注数据),以及在损失中改为我们需要尽量让未标注数据的分割区分不出来。
这篇文献本质上是进行了一个概念性扩展。第[1]篇文献讲了我们如何充分利用gt,让损失函数变成参数式的。这里巧妙地将gt变成了未标注数据,然后让损失函数去把未标注数据也纳入损失。这样会不会有一个问题就是让网络的表现变差了,它对未标注数据表现不变,然后把标注数据的表现变糟了呢?应该不至于。但是这种思想非常巧妙,它用的是gt,增强了对ground truth的一体化,而这里用的是未标注数据,纳入了未标注数据的特征,这是一个非常好的思路,要勇于借鉴学习。
注意文章中还有一些训练的tricks,一方面是采用concate操作融合特征,另一方面是输入的时候为了保证对图像的每一个部分都有反应,也就是对图像的3通道的每个channel都有$IP\ concate \ (1-I)P$,这样mix一下作为输入。
在超参数方面,作者这里给的超参数是一开始以分割为主,也就是$\lambda=0.1$,在一开始的30000个迭代中,然后把$\lambda$设置为1,但是lambda一般不能大于1,会造成不收敛。
关于主流的语义分割网络[3][4]
语义分割任务是图像识别的基本任务,也是一个多尺度稠密预测任务。FCN表示了现有的图像分类的神经网络结构可以直接套用在语义分割上,但是问题在于有哪些部分是可以省略的,有哪些结构真正起了用途?
本文提出了一个关于扩展卷积的概念解决了这个问题。注意我们的卷积操作本质上是公式: \(S(i,j)=\sum_{m,n}I(i-m,j-n)*Kernel(m,n)\) 本文提出的卷积是 \(S(i,j)=\sum_{m,n}I(i-l*m,j-l*n)Kernel(m,n)\) 当l大于1的时候就可以实现降采样。比如在文章的图片中,我们依次使用$l=1,2,4$的操作,就可以实现累计为15的感受野。怎么做的呢,假设有个$1515$的图片,用第一层的时候变成$1212$,第二层的时候本质是用了一个$55$的卷积核,变成了$77$,第三次用了一个$7*7$的卷积核,可以了。
这样就是感受野的来源。
这篇文章对一切还描述得很粗糙,但是文献[4]就不一样了。文献[4]提出了一个完整的分割结构并做出了扩展,分割结构如下:
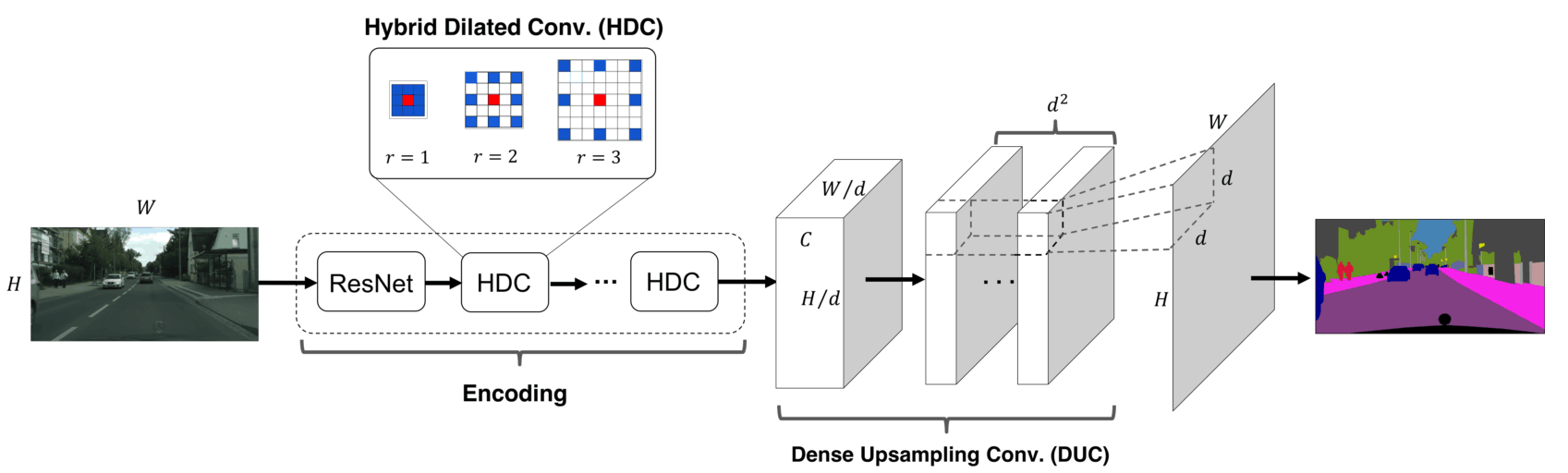
这里用的结构叫做HDC,是一个l分别为123的结构实现的降采样。
最后文章的resize是这样做的,假设经过了编码最后得到的图像大小是$W/d,H/d$,作者没有采用反卷积,而是采用了DUC的操作,简单来说,保持图像大小不变,增加了通道,对每一类增加了$d^2$个通道,最后按每一类把pixel重排到最后的图片。pytorch的函数nn.PixelShuffle可以达到这个目的,然后知乎文章文献4的笔记也可以做到这一点。
参考文献
[1]Semantic Segmentation using Adversarial Networks
[2]Deep Adversarial Networks for Biomedical Image Segmentation Utilizing Unannotated Images