2011年诺贝尔经济学奖获得者Thomas J. Sargent在世界科技创新论坛上表示,人工智能其实就是统计学,只不过用了一个很华丽的辞藻,其实就是统计学。自2014年来,以深度学习为代表的机器学习技术几乎成为了AI的代名词,而起源于统计学习方法的机器学习流派则可以看作是弱化了分布假设的应用统计学。
本文从回归方程出发对机器学习与深度学习的概念发展历史进行一段简单的介绍,旨在消除初学者无从下手的畏惧感,并对整个AI领域形成一种简洁而直观的理解。
本文主要参考资料为:
- Statistical Modeling: The Two Cultures
- Identifying and attacking the saddle point problem in high-dimensional non-convex optimization
- Deep Learning
从数据分布模型到算法模型
统计学有两个主流派别,一个是数据模型(data model),而另外一个则是算法模型(algorithm model)。Data model对采样数据$x$的分布做出假设(通常是正态性假设),用回归方式(线性回归,logit回归)来对目标$y$做出预测,最后用假设检验方法对模型参数进行检验。
线性回归模型的一般形式为
\[y = \beta_0+\sum_{m=1}^{M} \beta_mx_m +\epsilon\tag{1}\]假定我们有$n$组观测数据, 记作$(x_{i1},\ldots,x_{ip},y_i),i=1,\ldots,n$, 此时由这$n$组观测数据构建的的满足Gauss-Markov假设的线性回归模型为
\[\begin{aligned} y_i&=\beta_0 +\beta_1 x_{i1}+\ldots+\beta_p x_{ip} +e_i,i=1,\ldots,n\\ e_i &\text{ s.t. Gauss-Markov Assumption}\\ E(e_i)&=0\\ E(e_i^2)&=\sigma^2\\ E(e_ie_j)&=0(i\neq j) \end{aligned}\]按常规步骤(与计量经济学中一致),我们采用极大似然估计/最小二乘估计对参数进行估计,然后依据假设对系数进行显著性水平的F检验,最后对残差进行正态性检验。如果残差的正态性检验通过了$5\%$的置信度水平假设,那么模型就符合Gauss-Markov假设,模型关系在统计学意义上成立。
但是这种做法有一个致命的缺陷,就是残差检验只是对残差项的分布进行检验,但是无法检验我们的数据到底是不是线性模型所生成的。其实,模型的线性性检验一般是通过拟合优度检验来确定的:
\[R^2 = 1-\frac{RSS/(n-p-1)}{TSS/(n-1)} = \frac{\sum (\hat{y_i}-\bar{y})^2}{\sum (y_i-\bar{y})^2}*\frac{n-p-1}{n-1}\]如果$R^2$接近于1,那么我们就说模型的拟合能力好,这里一般就认为线性模型是成立的。拟合优度与残差检验构成了线性模型的基本逻辑基础。但是,这两个检验只对线性模型有效,如果模型中有非线性项则检验不成立。如果我们只考虑线性模型,那么一个显著的问题就是,这些检验的精度怎么样?
对于拟合优度检验,有很多研究表明,除非是模型极端的不fit数据,拟合度测试$R^2$才会reject。而对于残差分析而言,William Cleveland,残差分析的发明人之一,承认超过四维的数据,残差分析并不能测试出其真正的拟合程度,好的残差图也并不能说明数据很fit模型,这是因为,线性是一个很强的假设。一般来说,数据可以和多个模型同时匹配,因此单一的线性模型的难度在于,我们很难构造一个完整的模型,这个完整的模型包含了所有的备选线性模型。
同时我们以小见大,从上述线性模型的构建与检验过程,我们可以看出Data model的步骤一般是先假设数据的生成过程服从类似于$(1)$式的分布,然后进行数学推导和假设检验,最后对数据进行参数建模,根据模型给出结论,走上人生巅峰。
但是,对于数据建模的时候,一个很显然的问题就是,这样得出的结论是根据你设想的模型得出的,而不一定是真正的自然生成过程。设想的准确度依赖于拟合优度,残差分析等检验,但是这些检验的精度没有那么高,因此如果你的设想是错的,那么结论就是错的。
一直以来,由于最小二乘法在低维数据上极其少的计算量以及数据获取的困难,线性模型一直是主流模型。同时,由于高维优化问题以及计算能力的不足,预测前的第一步就是降维,避免维度灾难,即如果有过多的特征,那么首先要筛选出能表征绝大部分信息量的特征,进行降维。在线性回归,逻辑回归的实践中,一般都建议先进行特征选择。我们一般认为高维是危险的。统计学大佬Richard Bellman甚至对此有一个名句:
The curse of dimensionality(维数灾难)
但是最近的研究表明,维度不一定是curse,也有可能是blessing。同时,随着Computer Science与计算数学研究的进展,我们处理高维优化问题的时候有了许多行之有效的手段。比如,几年前有一个大佬通过统计物理的手段发现了高维优化问题的难点不是因为我们一直所认为的局部极小值很多,而是鞍点很多。这个发现是一语惊醒梦中人,至此之后许多针对该发现的优化算法提出,它们对于鞍点都有很好的处理方法。
对于高维优化算法一个非常好的入门综述文章An overview of gradient descent optimization algorithms,这个Blog分析了高维优化问题的主流算法与特点,并有可视化的过程。
在此基础上,统计学在数据模型的基础上又多了一个分支,即我们所讨论的算法模型(Algorithm Model)。这个模型主要手段是用尽量大的模型容量去拟合现有数据,典型代表为决策树,随机森林,随机条件场,以及最近的技术突破——深度学习算法。在这个阶段,模型的主要目的在于预测的准确度而不是预测的精度,因此,我们采用训练集-测试集来对模型进行检验。具体来说,我们用模型对训练集预测与训练集标签的差异(交叉熵)作为损失,而模型在训练中通过参数迭代来减少损失函数,同时模型的表现能力通过对测试集的预测与真值的残差来进行评估。这种模型的特点就是彻底放弃了对于数据的假设(包括对数据分布,生成情况的假设),同时放弃了对预测精度的评估(也就是不做置信区间估计),一切以准确率为主。
在2010年之前,随机森林,决策树,随机条件场都是广泛应用的技术。随机森林与决策树替代了线性模型,在整数数据拟合与多分类任务中取得了很好的效果,而随机条件场在自然语言的词性分析处理中应用广泛。同时,在单独的预测任务之外,数据分类,推荐算法与数据聚类算法等需求也衍生出一批新的算法,如SVM(支持向量机),K-means聚类算法,Active Learning(主动学习)算法等, 这些任务统称为机器学习任务,至此,统计学中的算法模型(algorithm model)发展为机器学习。
从机器学习到深度学习
深度学习的主要工具是机器学习的神经网络算法,而深度学习与机器学习的区别主要在于对于特征的认识。关于什么是特征,我们可以参考这篇文章。
一般的机器学习算法仍然有一个特点,就是我们仍然需要给出一些特征,而模型从数据中主动学习拟合的是这些特征的权重。以决策树为例,决策树的每一个子节点的二分类标准都是要人为给定的,我们要学习的是这些标准下的具体判定数值,或者这些标准在当前数据中的重要性程度,一个决策树的例子如下图所示:
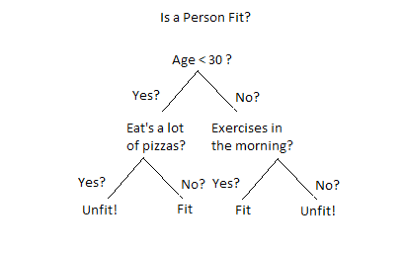
在这个例子中,我们要为一个人是否健康这个问题建模,判断所依据的几个节点Age,Eat’s pizzas,Exercises都是决策树中的特征,它依赖于我们人为给定,而特征的阈值如Age <30则令模型从数据中进行学习。
深度学习在机器学习的做法上更进一步,深度学习直接从原始输入出发,对特征本身与特征阈值都可以自主学习,省去了我们手动选择特征的过程。深度学习的核心数学定理是万能近似定理,即一个神经网络如果具有线性输出层和至少一层具有任何一种挤压性质的激活函数(比如sigmoid,ReLU这种把数值范围限定在很小部分之内)的隐藏层,那么只要给予网络足够数量的隐藏单元,那么它就可以以任意精度来近似任何从一个有限维空间到另一个有限维空间的Borel可测函数。这个定理意味着只要我们构建足够深的神经网络,那么它总能找出我们所需要的特征。这个定理是1990年发现的,但是神经网络在2010年才开始兴起,这是为什么呢?这里我们稍微讲一下神经网络的历史。
深度学习与神经网络,一段简史
自从1986年Hinton提出基于链式求导的反向传播算法对网络进行优化以来,神经网络事实上已经解决了参数拟合问题。但是一方面因为单层神经网络并不能将低维难以区分的区域投射到高维区域,而SVM支持向量积能解决这类问题,另一方面因为计算机算力不足,多层神经网络训练速度非常慢,无法迅速解决现有问题。
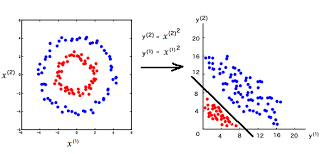
简单地来说,就是在这个阶段,机器学习算法比深度学习算法在训练时间与性能上都有压倒性的优势,因此深度学习算法式微,甚至变成了在学术界人人喊打的骗局。
改变发生在2006年。随着机器学习算法的成熟,人们不再局限于数字,而将目光转向了自然语言处理,图片与音频处理等方向。如果还记得的话,我们注意到机器学习的一个特征就是人为给定特征空间。但是因为这些新任务的特征空间是人所无法穷尽的,而我们所给出的特征往往并不能完整描述整个数据集的特征,这导致的一个极大的问题就是机器学习结果的False Positive率极大增加,也就是误报率很大。在2006年,Hinton又发了一篇文章指出,多隐层神经网络具有优越的直接学习特征的能力,而它在训练上的复杂度可以通过贪心算法,也就是固定其他层参数来逐层优化进行有效缓解。这篇论文可以说引燃了又一波深度学习的研究,因为它解决了神经网络训练资源的问题,以及提出了神经网络能够主动学习特征的理论。
同时期,在游戏厂商的推动下,GPU技术逐渐成熟了。如果是学过计算机图形学的同学一定对GPU不陌生。GPU着重于矩阵变换等数值计算方法,通过并行模式大大加快了纯数值计算的速度,而神经网络的优化迭代方法正适合采用GPU的并行算法来解决。GPU的大规模发展,使得高效训练深度神经网络成为可能,事实上现在通过Relu,DropOut以及Batch Normalization等手段,贪心优化法已经逐渐不再使用了。
而同时,经过充分训练的神经网络在目标检测与分类任务上取得了无可比拟的优势。2016年的Faster R-CNN框架下的多分类多实例目标检测在挑战赛上获得了73.2%的正确率,而同期最先进的机器学习算法只有23.3%。(这里的一个对比就是肉眼检测的准确率在70%左右,这基本可以说可以用啦).
一个用于分类的多层神经网络的例子放于Neural Network Playground上,我们可以直观地看到,深度学习技术就是把多个线性分类器叠加,从而逼近真实分类空间的过程。
卷积神经网络,机器视觉与模式识别
卷积神经网络是深度学习中的常用技术,其创始人LeCun获得了2018年的图灵奖。
卷积神经网络的卷积与数学中的卷积有什么区别呢?数学中的卷积公式为
\[s(t) = \int_{t_1}^t x(a)w(t-a)da\]这个公式可以直观的表示为如果我们要预测$t$时刻的一个数据,但是我们有$t_1−t$时刻的一系列时间序列数据,这些时间序列数据是有噪声的,为了充分利用这些数据,减少噪声的影响,我们定义一个加权函数$w(t)$,通过对这一系列数据的加权平均来得到$t$时刻确切的数据。这就是卷积运算。积分等价于求和,因此我们把积分形式离散化为
\[s(t)=\sum_{a=−\infty}^{\infty} x(a)w(t−a)\]这就是卷积神经网络所用的公式,卷积网络的运算过程是如下所述的动图
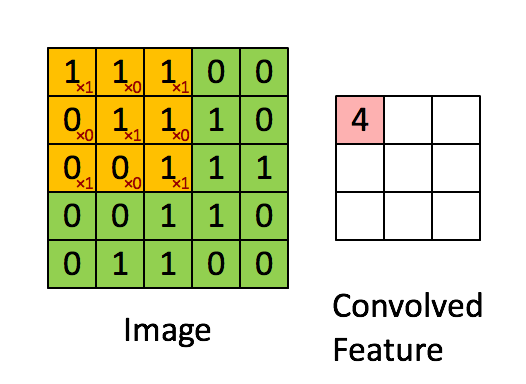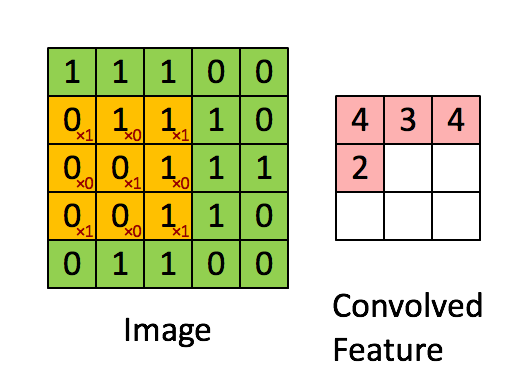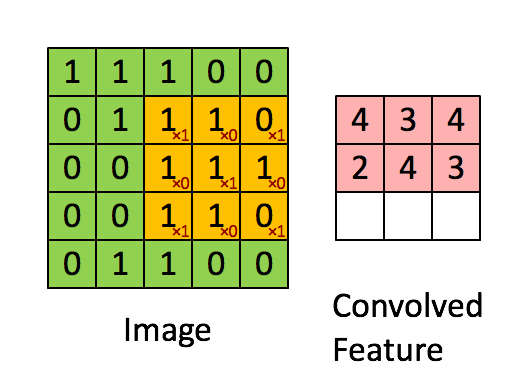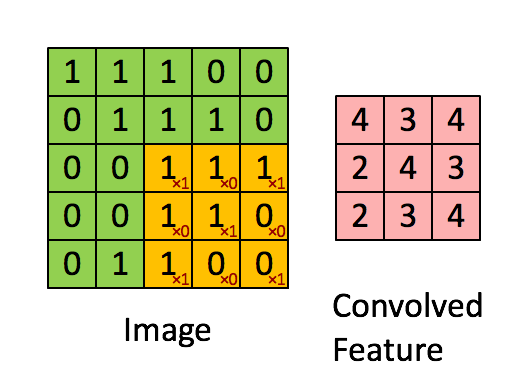
我们可以发现,卷积运算的一个好处就是空间不变性。一个卷积核代表一个特征,而在整张图上滑动的卷积运算使得只要这个特征在图中存在,相应的卷积核就能得到激活,激活的表现为输出的Feature值很大。